Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 4
Exercices
Travailler les automatismes
12 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'oral
Envie de réaliser ces exercices à l'oral ? Enregistrez-vous !
Enregistreur audio
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Quelle semble être la limite de la suite définie sur \mathbb{N} représentée ci‑dessous ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
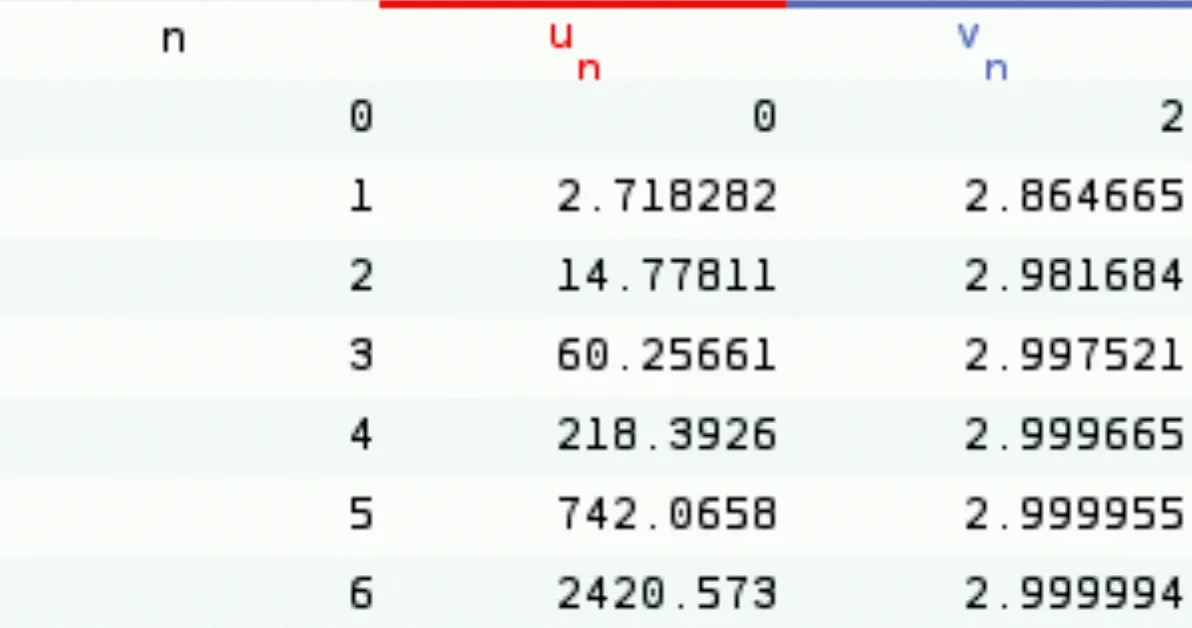
À l'aide de la calculatrice, on a calculé les premiers termes d'une suite (u_n) et d'une suite (v_n) définies sur \mathbb{N}. Quelle semble être la limite de chacune de ces suites ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
Conjecturer un majorant de la suite définie sur \mathbb{N} représentée ci‑dessous.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Conjecturer un majorant de la suite définie sur \mathbb{N} représentée ci‑dessous.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Utilisation de la définition d'une limite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Soit (w_n) la suite définie, pour tout entier naturel n non nul, par w_{n}=2+\frac{1}{\sqrt{n}}.
1. a. Déterminer le plus petit entier n_0 tel que, pour tout n \geqslant n_{0}, on a \left.w_{n} \in\right] 1{,}99 ; 2{,}01[.
b. Déterminer le plus petit entier n_1 tel que, pour tout n \geqslant n_{1}, on a \left|w_{n}-2\right| \leqslant 10^{-4}.
c. Soit \varepsilon un nombre réel strictement positif. Déterminer le plus petit entier n_2 tel que, pour tout n \geqslant n_{2}, on a \left.w_{n} \in\right] 2-\varepsilon ; 2+\varepsilon[.
2. En déduire \lim\limits_{\substack{n \to +\infty}} w_{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Soit (u_n) la suite définie, pour tout entier naturel n, par u_{n}=3 n-4.
1. a. Déterminer le plus petit entier n_0 tel que, pour tout n \geqslant n_{0}, on a u_{n} \geqslant 100.
b. Déterminer le plus petit entier n_1 tel que, pour tout n \geqslant n_{1}, on a u_{n} \geqslant 1 000.
c. Soit \text{A} un nombre réel. Déterminer le plus petit entier n_2 tel que, pour tout n \geqslant n_{2}, on a u_{n} \geqslant \mathrm{A}.
2. En déduire \lim\limits_{\substack{n \to +\infty}} u_{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Soit (v_n) la suite définie, pour tout entier naturel n, par v_{n}=-5 n^{2}.
1. a. Déterminer le plus petit entier n_0 tel que, pour tout n \geqslant n_{0}, on a v_{n} \leqslant -720.
b. Déterminer le plus petit entier n_1 tel que, pour tout n \geqslant n_{1}, on a v_{n} \leqslant -3 125.
c. Soit \text{A} un nombre réel. Déterminer le plus petit entier n_2 tel que, pour tout n \geqslant n_2, on a v_{n} \leqslant \mathrm{A}.
2. En déduire \lim\limits_{\substack{n \to +\infty}} v_{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Majorants, minorants
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
1. Montrer que la suite (u_n) définie, pour tout entier naturel n, par u_{n}=\frac{2 n+3}{n+2} est majorée par 2.
2. Montrer que la suite (v_n) définie, pour tout entier naturel n, par v_{n}=\frac{n^{2}+(-1)^{n}}{n+1} est minorée par 0.
3. Montrer que la suite (w_n) définie, pour tout entier naturel n, par w_{n}=\sqrt{n+1}-\sqrt{n} est minorée par 0 et majorée par 1.
4. Montrer par récurrence que la suite (t_n) définie par t_{0}=-\sqrt{2} et, pour tout entier naturel n, t_{n+1}=\frac{1}{4} t_{n}-2 est minorée par -3 et majorée par -1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Opérations sur les limites
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans chaque cas, donner, si elle existe, la limite de la suite dont on donne le terme général.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
1. r_{n}=\sqrt{n}+n^{2}
2. s_{n}=3+\frac{1}{n^{4}}
3. t_{n}=\left(\frac{4}{3}\right)^{n}+\frac{1}{n^{2}}
4. u_{n}=\frac{1}{\sqrt{n}}-n^{3}
5. v_{n}=-\left(n+\pi^{n}\right)
6. w_{n}=-4+\left(\frac{7}{10}\right)^{n}+n^{5}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
1. r_{n}=n^{2}-n
2. s_{n}=-n+\sqrt{n}
3. t_{n}=-\left(-\sqrt{n}+n^{7}\right)
4. u_{n}=-\left(n^{6}-n^{3}\right)
5. v_{n}=n^{5}-n^{3}+n
6. w_{n}=n^{6}-n^{4}+n^{2}-n
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
1. r_{n}=\left(n^{5}+4\right)(n-3)
2. s_{n}=5 \times\left(\frac{185}{192}\right)^{n}
3. t_{n}=(8 n-2)\left(3+\frac{1}{\sqrt{n}}\right)
4. u_{n}=-2 \times\left(\frac{144}{121}\right)^{n}
5. v_{n}=\left(6-n^{4}\right)\left(\frac{1}{n^{3}}+7\right)
6. w_{n}=\left(4-n^{7}\right)\left(n^{9}+1\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
1. t_{n}=\frac{1}{n^{2}}(2 n+4)
2. u_{n}=\frac{1}{n}(2 n+4)
3. v_{n}=\frac{1}{n^{4}}\left(n^{3}+2 n^{2}\right)
4. w_{n}=\frac{1}{\sqrt{n}}(-n-\sqrt{n})
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
1. t_{n}=\frac{1}{n^{5}}\left(-8-n^{6}\right)
2. u_{n}=\frac{1}{n}\left(-n^{3}+3\right)
3. v_{n}=\frac{1}{\sqrt{n}}(2 n-3)
4. w_{n}=\frac{1}{n^{3}}\left(1-n^{3}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
1. r_{n}=\frac{2}{n^{2}-4}
2. s_{n}=\frac{n^{3}}{4+\frac{1}{n}}
3. t_{n}=\frac{4-\frac{1}{\sqrt{n}}}{\frac{1}{n^{3}}-6}
4. u_{n}=\frac{1}{\left(\frac{4}{3}\right)^{n}}
5. v_{n}=\frac{-n}{\left(\frac{3}{4}\right)^{n}}
6. w_{n}=\frac{\left(\frac{5}{7}\right)^{n}}{\frac{1}{n^{2}}-9}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
1. r_{n}=\frac{3 n^{2}+4}{2 n+2}
2. s_{n}=\frac{\left(\frac{7}{5}\right)^{n}}{\left(\frac{4}{3}\right)^{n}}
3. t_{n}=\frac{2 n-4}{7-3 n}
4. u_{n}=\frac{12 n^{2}}{5 n^{7}}
5. v_{n}=\frac{\left(\frac{3}{5}\right)^{n}}{\left(\frac{2}{3}\right)^{n}}
6. w_{n}=\frac{n^{2}-1}{n+1}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
1. r_{n}=\frac{4-5 n}{2 n^{2}+1}
2. s_{n}=\frac{\left(\frac{6}{19}\right)^{n}}{\left(\frac{4}{11}\right)^{n}}
3. t_{n}=\frac{-6 n^{2}+3}{-n-2 n^{2}}
4. u_{n}=\frac{\left(\frac{18}{5}\right)^{n}}{\left(\frac{16}{11}\right)^{n}}
5. v_{n}=\frac{n^{2}+n+1}{n^{3}}
6. w_{n}=\frac{n^{2}-4}{n+2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorèmes de comparaison
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
1. Soit (u_n) une suite telle que, pour tout entier naturel n, u_{n} \geqslant n^{2}+1. Déterminer \lim\limits_{\substack{n \to +\infty}} u_{n}.
2. Soit (v_n) une suite telle que, pour tout entier naturel n, v_{n} \leqslant-3 n-4. Déterminer \lim\limits_{\substack{n \to +\infty}} v_{n}.
3. Soit (w_n) une suite telle que, pour tout entier naturel n, -1+2 n \leqslant w_{n} \leqslant 1+2 n. Déterminer \lim\limits_{\substack{n \to +\infty}} w_{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Justifier que, pour tout entier naturel n, \sqrt{n^{3}+1} \geqslant n \sqrt{n}. En déduire \lim\limits_{\substack{n \to +\infty}} \sqrt{n^{3}+1}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
Soit (t_n) la suite définie par t_0=5 et, pour tout entier naturel n, t_{n+1}=t_{n}-5 n-4.
1. Montrer par récurrence que, pour tout entier n \geqslant 2, t_{n} \leqslant-n^{2}.
2. En déduire \lim\limits_{\substack{n \to +\infty}} t_{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
Soit (u_n) la suite définie, pour tout entier naturel n, par u_{n}=0{,}59^{n}\left(5+(-1)^{n}\right).
1. Pour tout entier naturel n, déterminer un encadrement de u_n.
2. En déduire \lim\limits_{\substack{n \to +\infty}} u_{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
Soit (v_n) la suite définie pour tout entier n \geqslant 1 par v_{n}=\frac{\sin (n)}{n^{3}}.
1. Pour tout n \geqslant 1, déterminer un encadrement de v_n.
2. En déduire \lim\limits_{\substack{n \to +\infty}} v_{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices inversés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
Déterminer cinq suites distinctes dont les limites sont égales à 4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
On lit le raisonnement suivant :
« On a u_{n} \leqslant w_{n} \leqslant v_{n} et \lim\limits_{\substack{n \to +\infty}} u_{n}=\lim\limits_{\substack{n \to +\infty}} v_{n}=-5 donc \lim\limits_{\substack{n \to +\infty}} w_{n}=-5. »
Compléter le raisonnement et écrire un énoncé possible correspondant à cette résolution d'exercice.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah