Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 4
Entraînement 1
Limites finies
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
Flash
Déterminer les limites des suites ci-dessous.
1. r_{n}=\frac{1}{n^{2}}
2. s_{n}=\frac{1}{\sqrt{n}}
3. t_{n}=\frac{1}{n^{8}}
2. s_{n}=\frac{1}{\sqrt{n}}
3. t_{n}=\frac{1}{n^{8}}
4. u_{n}=\left(\frac{7}{9}\right)^{n}
5. v_{n}=\left(\frac{17}{21}\right)^{n}
6. w_{n}=n^{-7}
5. v_{n}=\left(\frac{17}{21}\right)^{n}
6. w_{n}=n^{-7}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
Flash
À l'aide de la calculatrice, déterminer le plus petit entier n_0 tel que, pour tout n \geqslant n_{0}, on a : \frac{-2 n^{4}+3 n \sqrt{n}-6}{6 n^{4}} \in\left]-0{,}334 ;-0{,}333\right[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
Flash
À l'aide de la calculatrice, déterminer le plus petit entier n_0 tel que, pour tout n \geqslant n_{0}, on a : \frac{3 n^{2}-8 n+12}{24 n^{2}} \in \left]0{,}12\, ; 0{,}13\right[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
[Calculer.]
Soit (u_n) la suite définie, pour tout entier n \geqslant 1, par : u_{n}=\frac{4 n^{2}-2}{n^{2}}.
1. Les premiers termes de la suite(u_n) sont représentés ci‑dessous.
Conjecturer la limite de la suite (u_n).
1. Les premiers termes de la suite(u_n) sont représentés ci‑dessous.
Le zoom est accessible dans la version Premium.
2. Montrer que, pour tout entier n \geqslant 1, on a u_{n}=4-\frac{2}{n^{2}}.
3. Démontrer la conjecture émise à la question 1.
3. Démontrer la conjecture émise à la question 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
[Calculer.]
Soit (v_n) la suite définie, pour tout entier naturel n, par v_{n}=\frac{-6 n-2}{2 n+3}.
1. Montrer que, pour tout entier naturel n, on a : v_{n}=-3+\frac{7}{2 n+3}.
2. Montrer que la limite de (v_n) est -3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
Python
[Modéliser.]
On considère la suite (u_n) définie par u_0=2{,}5 et, pour tout entier naturel n, u_{n+1}=-u_{n}^{2}+5 u_{n}-3.
On donne la fonction ci‑dessous.
def fonction(e): N = 0 U = 2.5 while abs(U - 3) >= e: N = N + 1 U = -U**2 + 5*U - 3 return(N)
1. a. Quelle est la valeur renvoyée lors de l'appel fonction(0.1) ?
b. Quelle est la valeur renvoyée lors de l'appel fonction(0.001) ?
2. De manière générale, quelle est la valeur renvoyée lors de l'appel fonction(e) ?
3. Quelle conjecture peut‑on émettre quant à la limite de la suite (u_n) ?
b. Quelle est la valeur renvoyée lors de l'appel fonction(0.001) ?
2. De manière générale, quelle est la valeur renvoyée lors de l'appel fonction(e) ?
3. Quelle conjecture peut‑on émettre quant à la limite de la suite (u_n) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
Python
[Modéliser.]
On considère la suite (w_n) définie par w_0=5 et, pour tout entier naturel n, w_{n+1}=\sqrt{\frac{1}{w_{n}}}.
On donne la fonction ci‑dessous.
from math import* def fonction(e): N = 0 W = 5 while abs(W - 1) >= e: N = N + 1 W = sqrt(1/W) return(N)
1. a. Quelle est la valeur renvoyée lors de l'appel fonction(0.001) ?
b. Quelle est la valeur renvoyée lors de l'appel fonction(0.00001) ?
2. De manière générale, quelle est la valeur renvoyée lors de l'appel fonction(e) ?
3. Quelle conjecture peut‑on émettre quant à la limite de la suite (w_n) ?
b. Quelle est la valeur renvoyée lors de l'appel fonction(0.00001) ?
2. De manière générale, quelle est la valeur renvoyée lors de l'appel fonction(e) ?
3. Quelle conjecture peut‑on émettre quant à la limite de la suite (w_n) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
Vrai/Faux
[Raisonner.]
Les justifications suivantes sont‑elles vraies ou fausses ? Justifier.
1. Si (u_n) est une suite bornée, alors elle converge.
2. Si (v_n) est une suite convergente, alors elle est bornée.
3. Si (w_n) est une suite croissante et majorée par \text{M}, alors elle converge vers \text{M}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Tableur
[Raisonner.]
On considère la suite (t_n) définie par t_0=5 et, pour tout entier naturel n, t_{n+1}=\frac{1}{3} t_{n}+2.
1. Les premières valeurs de la suite (t_n) ont été calculées à l'aide d'un tableur dont voici une capture d'écran.
Le zoom est accessible dans la version Premium.
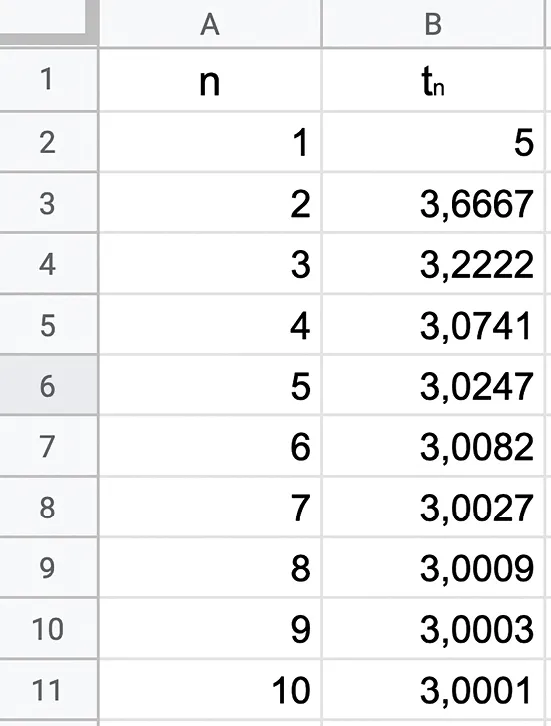
a. Trouver la formule à saisir dans la cellule B3 puis à étirer vers le bas pour obtenir les valeurs des premiers termes de la suite (t_n).
b. Quelle conjecture peut‑on faire sur les variations de la suite (t_n) ?
c. Quelle conjecture peut‑on faire sur la limite de la suite (t_n) ?
b. Quelle conjecture peut‑on faire sur les variations de la suite (t_n) ?
c. Quelle conjecture peut‑on faire sur la limite de la suite (t_n) ?
2. Montrer que, pour tout entier naturel n, 0\lt t_{n+1}\lt t_{n}.
3. Justifier que la suite (t_n) converge.
4. Soit \ell la limite de la suite (t_n). On admet que \ell vérifie \ell=\frac{1}{3} \ell+2. Déterminer la valeur de \ell.
3. Justifier que la suite (t_n) converge.
4. Soit \ell la limite de la suite (t_n). On admet que \ell vérifie \ell=\frac{1}{3} \ell+2. Déterminer la valeur de \ell.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
Tableur
[Raisonner.]
On considère la suite (r_n) définie par r _0=1 et, pour tout entier naturel n, r_{n+1}=\frac{r_{n}}{\sqrt{r_{n}^{2}+1}}.
1. Les premières valeurs de la suite (r_n) ont été calculées à l'aide d'un tableur dont voici une capture d'écran.
Le zoom est accessible dans la version Premium.
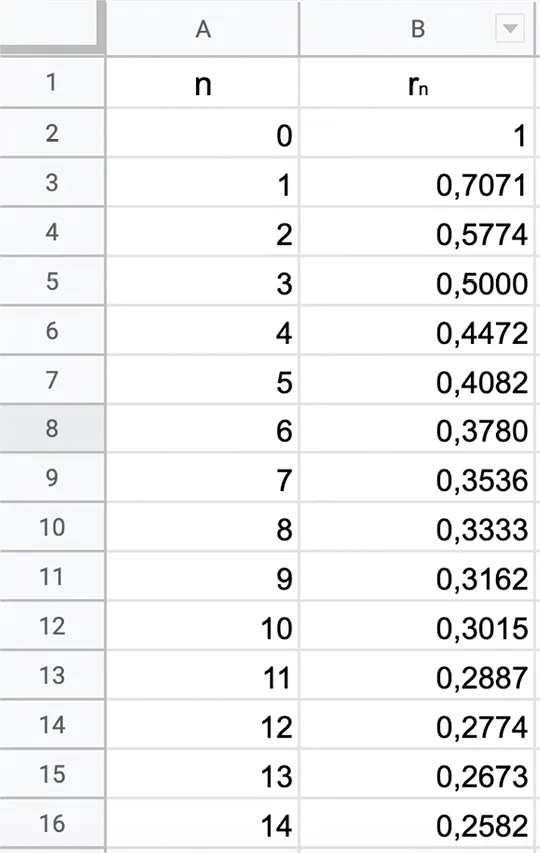
a. Trouver la formule à saisir dans la cellule B3 puis à étirer vers le bas pour obtenir les valeurs des premiers termes de la suite (r_n).
b. Quelle conjecture peut‑on faire sur les variations de la suite (r_n) ?
c. Quelle conjecture peut‑on faire sur la limite de la suite (r_n) ?
b. Quelle conjecture peut‑on faire sur les variations de la suite (r_n) ?
c. Quelle conjecture peut‑on faire sur la limite de la suite (r_n) ?
2. Montrer que, pour tout entier naturel n, 0\lt r_{n} \leqslant 1.
3. Déterminer le sens de variation de la suite (r_n).
4. Justifier que la suite (r_n) converge.
5. Soit \ell la limite de la suite (r_n). On admet que \ell vérifie \ell=\frac{\ell}{\sqrt{\ell^{2}+1}}. Déterminer la valeur de \ell.
3. Déterminer le sens de variation de la suite (r_n).
4. Justifier que la suite (r_n) converge.
5. Soit \ell la limite de la suite (r_n). On admet que \ell vérifie \ell=\frac{\ell}{\sqrt{\ell^{2}+1}}. Déterminer la valeur de \ell.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
La constante d'Apéry
[Raisonner.]
Soit (u_n) la suite définie pour tout entier n \geqslant 1 par u_{n}=\mathop{\sum}\limits_{k=1}\limits^{n} \frac{1}{k^{3}}=\frac{1}{1^{3}}+\frac{1}{2^{3}}+\ldots+\frac{1}{n^{3}}. 1. Montrer que la suite (u_n) est croissante.
u_{n} \leqslant 2-\frac{1}{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La limite de cette suite est appelée la constante d'Apéry et vaut environ 1,202 056 90. Elle doit son nom au mathématicien français Roger Apéry qui a prouvé en 1978 que ce nombre est irrationnel, deux ans après la publication d'un manifeste, Mathématiques constructives, défendant une philosophie originale des mathématiques. Apéry était également engagé politiquement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
Python
[Modéliser.]
D'après bac L/ES, Polynésie, septembre 2014
Une personne décide d'ouvrir un compte épargne le 1er janvier 2014 et d'y placer 2 000 €. Le placement à intérêts composés est au taux annuel de 3 %. Elle verse 150 € sur ce compte chaque 1er janvier de l'année suivante.
Pour tout entier naturel n, on note u_n le montant présent sur ce compte au 1er janvier de l'année 2014 + n après le versement de 150 €. On a u_0=2 000. Dans tout l'exercice, les résultats seront arrondis à 10^{-2} près.
1. Combien d'argent cette personne aura‑t‑elle sur son compte épargne en 2015 puis en 2016 ?
2. Justifier que, pour tout entier naturel n, on a : u_{n+1}=1{,}03 u_{n}+150.
3. Pour tout entier n, on pose v_n=u_n+5 000.
Démontrer que la suite (v_n) est une suite géométrique de raison 1{,}03.
4. Exprimer v_n en fonction de n et en déduire que, pour tout nombre entier n, on a : u_{n}=7 000 \times 1{,}03^{n}-5 000.
5. Déterminer la limite de (u_n).
6. On considère le programme ci‑contre.
Le zoom est accessible dans la version Premium.
a. Quelle est la valeur renvoyée lors de l'appel programme(4000) ?
b. Interpréter cette valeur dans le contexte de l'énoncé.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah