Problème

31

Optique au secours de la cinématique

✔ RAI/ANA : Construire un raisonnement
✔ COM : Rédiger correctement une résolution d’exercice

Un sauveteur en mer, assimilé à un point $\text{A}$, aperçoit un touriste, assimilé à un point $\text{B}$, qui se noie. Il se met alors à courir dans sa direction sur la plage à la vitesse constante $v$, puis nage à la vitesse $\alpha \cdot v$ avec $\alpha \lt 1$, ce qui confère au sauveteur une vitesse de nage en mer plus faible. Le sauveteur doit optimiser le trajet emprunté pour secourir le plus rapidement possible le touriste en train de se noyer.

Questions préliminaires

1. Exprimer la durée de course sur le sable, notée $\Delta t_{\text{sable}}$, en fonction de $y_\text{A},\ x$ et $v$.


2. Exprimer la durée de nage en mer, notée $\Delta t_{\text{mer}}$, en fonction de $x_\text{B},\ y_\text{B}, \ x$ et $\alpha \cdot v$.


Problème

3. Établir la relation entre les angles $i_1$ et $i_2$ pour que la durée du trajet du sauveteur soit minimale.

Doc. 1

Principe de Fermat pour sauveteur en mer

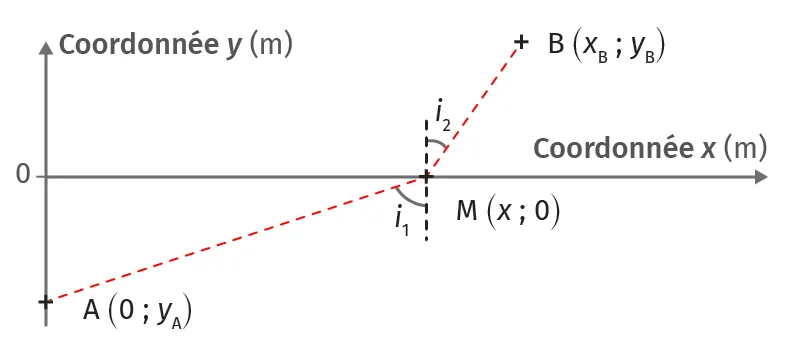
Doc. 2

Schématisation de la situation

Doc. 3

Formulaire mathématique

Une fonction admet un extremum (maximum ou minimum) lorsque sa dérivée s’annule.

La fonction $f(x) = a \cdot \sqrt{g(x)}$ admet comme dérivée :

$f'(x) = a \cdot \dfrac{g'(x)}{2\sqrt{g(x)}}$

Retrouvez un autre problème sur la plage en cliquant ici.

32

Accélération en rotation

✔ RAI/ANA : Construire un raisonnement



1. Calculer la vitesse de Thomas Pesquet lorsqu’il subit l’accélération maximale.


2. Lors d’un mouvement rectiligne, avec un départ arrêté, déterminer la vitesse atteinte par un spationaute à l’entraînement subissant une accélération de 9 $g$ en 1,0 s.


3. Expliquer quel est l’intérêt d’un entraînement en mouvement circulaire.

• Accélération correspondant à 1 $g$ : $a_{\text{1 g}} = 9{,}81$ m·s^-2
• Longueur du bras de la centrifugeuse : $R = 18$ m

Retrouvez une vidéo de l'astronaute Chris Hadfield dans une centrifugeuse en cliquant ici.