Chapitre 11
Cours
Description d'un mouvement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Référentiel et nature du mouvement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour simplifier l'étude du mouvement d'un système, on s'intéresse uniquement aux coordonnées d'un point matériel, noté \text{M}.
L'association d'une horloge est nécessaire pour pouvoir étudier l'évolution temporelle du mouvement.
Un référentiel est un objet pris comme référence pour la description du mouvement associé à un repère. Il permet de définir les positions lors de l'étude.
Un repère est défini par un point d'origine \text{O} auquel est associée une base orthonormée.
Un repère est défini par un point d'origine \text{O} auquel est associée une base orthonormée.
L'association d'une horloge est nécessaire pour pouvoir étudier l'évolution temporelle du mouvement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Un référentiel n'est pas un repère et vice versa.
- Un référentiel est un objet pris comme référence.
- Un repère est une base vectorielle munie d'une origine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Étude du mouvement de la Lune


Le mouvement de la Lune peut être étudié dans un référentiel géocentrique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Position, vitesse et accélération
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AVecteur position
Dans l'espace, le point \text{M} se repère à l'aide du vecteur position \overrightarrow{\text{OM}}(t) dont les coordonnées cartésiennes sont notées :
L'ensemble des positions occupées par le point M au cours du temps constitue la trajectoire. De nombreux mouvements peuvent être ramenés à une étude plane, c'est-à-dire à deux dimensions.
\overrightarrow{\text{OM}}(t)
\begin{pmatrix}
x(t) \\
y(t) \\
z(t)
\end{pmatrix}_{(\text{O}, \ \overrightarrow{i},\ \overrightarrow{j}, \ \overrightarrow{k})}
x(t) : abscisse du point M
y(t) : ordonnée du point M
z(t) : altitude du point M
y(t) : ordonnée du point M
z(t) : altitude du point M
L'ensemble des positions occupées par le point M au cours du temps constitue la trajectoire. De nombreux mouvements peuvent être ramenés à une étude plane, c'est-à-dire à deux dimensions.
Dans ces cas-là, on exprimera simplement :
\overrightarrow{\text{OM}}(t)
\begin{pmatrix}
x(t) \\
y(t)
\end{pmatrix}_{(\text{O}, \ \overrightarrow{i},\ \overrightarrow{j})}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Vecteur position

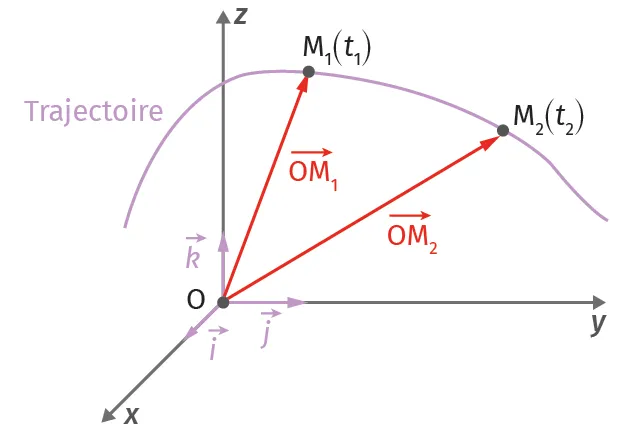
La position du point \text{M} évolue au cours du temps : la trajectoire se dessine peu à peu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BVecteur vitesse
Le vecteur vitesse est défini comme la dérivée du vecteur position :
a. Dans un repère cartésien
En coordonnées cartésiennes, les coordonnées du vecteur vitesse v sont définies comme les dérivées temporelles des coordonnées du vecteur position :
La norme v de \vec{v} à la date t est donnée par la relation :
b. Dans un repère de Frenet
Pour les mouvements circulaires, l'étude cinématique du point \text{M} en coordonnées cartésiennes est complexe et fait intervenir les fonctions trigonométriques. Le repère de Frenet, centré sur M, permet de contourner cette difficulté. On lui associe deux vecteurs :
\vec{v} = \dfrac{\text{d} \overrightarrow{\text{OM}}}{\text{d}t}
a. Dans un repère cartésien
En coordonnées cartésiennes, les coordonnées du vecteur vitesse v sont définies comme les dérivées temporelles des coordonnées du vecteur position :
\vec{v}(t)
\begin{pmatrix}
v_x(t) = \dfrac{\text{d}x}{\text{d}t} \\
v_y(t) = \dfrac{\text{d}y}{\text{d}t} \\
v_z(t) = \dfrac{\text{d}z}{\text{d}t}
\end{pmatrix}_{(\text{O}, \ \overrightarrow{i}, \ \overrightarrow{j}, \ \overrightarrow{k})}
La norme v de \vec{v} à la date t est donnée par la relation :
v = \sqrt{v_x^2 + v_y^2 + v_z^2}
b. Dans un repère de Frenet
Pour les mouvements circulaires, l'étude cinématique du point \text{M} en coordonnées cartésiennes est complexe et fait intervenir les fonctions trigonométriques. Le repère de Frenet, centré sur M, permet de contourner cette difficulté. On lui associe deux vecteurs :
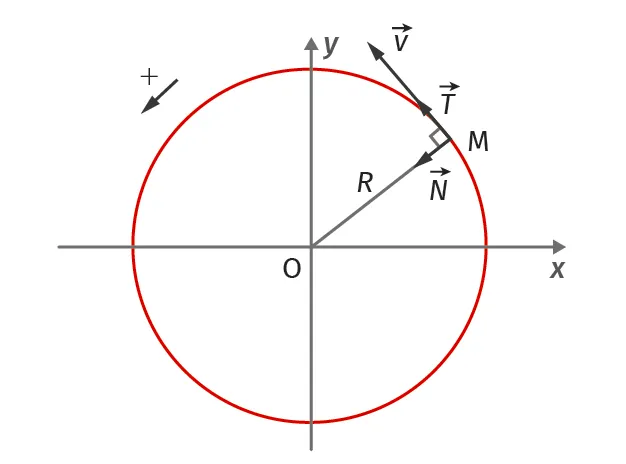
\overrightarrow{T} : vecteur unitaire tangent à la trajectoire, orienté dans le sens du mouvement ;
\overrightarrow{N} : vecteur unitaire, orthogonal à la trajectoire et dirigé vers le centre de la courbure.
Dans le repère de Frenet, le vecteur vitesse \vec{v}(t) s'exprime :
\overrightarrow{N} : vecteur unitaire, orthogonal à la trajectoire et dirigé vers le centre de la courbure.
Dans le repère de Frenet, le vecteur vitesse \vec{v}(t) s'exprime :
\vec{v}(t)
\begin{pmatrix}
v(t) \\
0
\end{pmatrix}_{(\text{M}, \ \overrightarrow{T}, \ \overrightarrow{N})}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Notation des vecteurs
Parfois, le vecteur position peut être exprimé de manière plus compacte comme une combinaison linéaire des vecteurs \vec{i}, \vec{j} et \vec{k} :
De la même manière, on pourra également utiliser ce type de notation pour les vecteurs vitesse et accélération.
\overrightarrow{\text{OM}}(t) = x(t) \cdot \vec{i} + y(t) \cdot \vec{j} + z(t) \cdot \vec{k}
De la même manière, on pourra également utiliser ce type de notation pour les vecteurs vitesse et accélération.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- La notation \dfrac{\text{d}f}{\text{d}t} est équivalente à la notation f'(t) en mathématiques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4Vecteur vitesse
Le vecteur vitesse moyen \vec{v}_\text{moy} correspond au rapport entre la variation du vecteur position et la durée de la variation :
En considérant une durée infiniment faible, on aboutit à la notion de dérivée :
\vec{v} = \lim \limits_{\Delta t \rightarrow 0} \dfrac{\overrightarrow{\text{OM}}(t + \Delta t) - \overrightarrow{\text{OM}}(t)}{\Delta t}
\vec{v} = \dfrac{\text{d}\overrightarrow{\text{OM}}(t)}{\text{d}t}
\vec{v}_\text{moy} = \dfrac{\overrightarrow{\text{OM}}(t + \Delta t) - \overrightarrow{\text{OM}}(t)}{\Delta t}
En considérant une durée infiniment faible, on aboutit à la notion de dérivée :
\vec{v} = \lim \limits_{\Delta t \rightarrow 0} \dfrac{\overrightarrow{\text{OM}}(t + \Delta t) - \overrightarrow{\text{OM}}(t)}{\Delta t}
\vec{v} = \dfrac{\text{d}\overrightarrow{\text{OM}}(t)}{\text{d}t}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CVecteur accélération
Le vecteur accélération est défini comme la dérivée temporelle du vecteur vitesse et par conséquent comme la dérivée seconde du vecteur position par rapport au temps :
a. Dans un repère cartésien
En coordonnées cartésiennes, le vecteur accélération \vec{a}(t) correspond à :
Ces coordonnées correspondent aux dérivées temporelles des coordonnées de la vitesse ou comme les dérivées secondes des coordonnées du vecteur position :
La norme du vecteur accélération se calcule à partir de :
b. Dans un repère de Frenet
Pour les mouvements étudiés dans le repère de Frenet, l'accélération possède deux composantes :
\vec{a} = \dfrac{\text{d}v}{\text{d}t} \cdot \overrightarrow{T} + \dfrac{v^2}{R} \cdot \overrightarrow{N} ou \vec{a} \begin{pmatrix} \dfrac{\text{d}v}{\text{d}t} \\ \dfrac{v^2}{R} \end{pmatrix}_{(\text{M}, \ \overrightarrow{T}, \ \overrightarrow{N})}
R : rayon de la trajectoire circulaire (m)
\vec{a} = \dfrac{\text{d} \vec{v}}{\text{d}t} = \dfrac{\text{d}^2 \overrightarrow{\text{OM}}}{\text{d}t^2}
a. Dans un repère cartésien
En coordonnées cartésiennes, le vecteur accélération \vec{a}(t) correspond à :
\vec{a}(t)
\begin{pmatrix}
a_x(t) \\
a_y(t) \\
a_z(t)
\end{pmatrix}_{(\text{O}, \ \overrightarrow{i}, \ \overrightarrow{j}, \ \overrightarrow{k})}
Ces coordonnées correspondent aux dérivées temporelles des coordonnées de la vitesse ou comme les dérivées secondes des coordonnées du vecteur position :
\vec{a}(t)
\begin{pmatrix}
a_x(t) = \dfrac{\text{d}v_x}{\text{d}t} \\
a_y(t) = \dfrac{\text{d}v_y}{\text{d}t} \\
a_z(t) = \dfrac{\text{d}v_z}{\text{d}t}
\end{pmatrix}_{(\text{O}, \ \overrightarrow{i}, \ \overrightarrow{j}, \ \overrightarrow{k})}
=
\begin{pmatrix}
a_x(t) = \dfrac{\text{d}^2x}{\text{d}t^2} \\
a_y(t) = \dfrac{\text{d}^2y}{\text{d}t^2} \\
a_z(t) = \dfrac{\text{d}^2z}{\text{d}t^2}
\end{pmatrix}_{(\text{O}, \ \overrightarrow{i}, \ \overrightarrow{j}, \ \overrightarrow{k})}
La norme du vecteur accélération se calcule à partir de :
a = \sqrt{a_x^2 + a_y^2 + a_z^2}
b. Dans un repère de Frenet
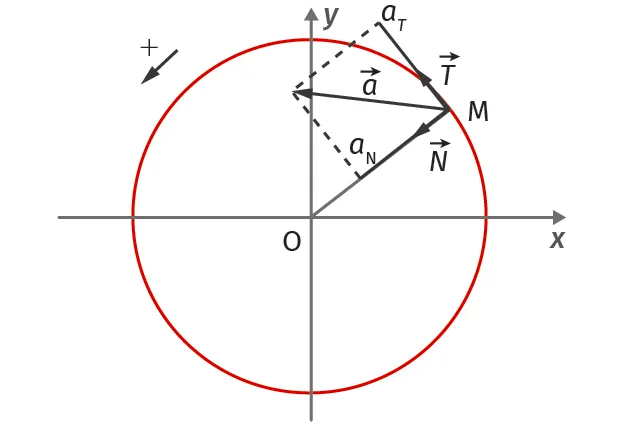
Pour les mouvements étudiés dans le repère de Frenet, l'accélération possède deux composantes :
- une composante tangentielle a_\text{T} qui caractérise les variations temporelles de la valeur de la vitesse ;
- une composante normale a_\text{N} liée à la vitesse et à la géométrie de la trajectoire, qui caractérise les variations temporelles de direction du vecteur vitesse.
\vec{a} = \dfrac{\text{d}v}{\text{d}t} \cdot \overrightarrow{T} + \dfrac{v^2}{R} \cdot \overrightarrow{N} ou \vec{a} \begin{pmatrix} \dfrac{\text{d}v}{\text{d}t} \\ \dfrac{v^2}{R} \end{pmatrix}_{(\text{M}, \ \overrightarrow{T}, \ \overrightarrow{N})}
R : rayon de la trajectoire circulaire (m)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Norme, valeur et intensité sont des synonymes couramment employés.
- La norme d'un vecteur est toujours positive, tandis que la composante d'un vecteur peut être positive ou négative.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5Lancer de marteau


Kibwé Johnson, champion de lancer de marteau de l'USATF en 2014, exerce une action mécanique mettant le boulet en mouvement circulaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 6Vecteur vitesse dans le repère de Frenet

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 7Vecteur accélération dans le repère de Frenet

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Les notations v_x(t) et \dfrac{\text{d}x}{\text{d}t} sont équivalentes.
- Elles représentent la composante du vecteur vitesse \vec{v} sur l'axe (\text{O}_x).
- Elles peuvent être positives (\text{M} se déplace dans le sens de \vec{i}) ou négatives (\text{M} se déplace à l'opposé de \vec{i}).
- Il en est de même pour les composantes sur les axes (\text{O}y) et (\text{O}z).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Études de quelques cas courants
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AMouvements rectilignes
La trajectoire d'un mouvement rectiligne est une droite. En conséquence, le repère (O, \vec{i}, \vec{j}, \vec{k}) se réduit au seul axe (\text{O}x) de vecteur unitaire \vec{i} pour un mouvement horizontal. Les descripteurs du mouvement sont donc réduits à leur seule composante suivant l'axe (\text{O}x) :
a. Mouvement rectiligne uniforme
Ainsi, dans le cas du mouvement rectiligne uniforme, on peut écrire :
Pour les mouvements rectilignes, la coordonnée x(t) a quant à elle pour forme :
x(t) = v \cdot t + x_0 où
x_0 : coordonnée initiale du système (m)
Cette équation peut être déduite à partir de la recherche d'une primitive de v(t).
➜ .
b. Mouvement rectiligne uniformément accéléré
Cette accélération constante implique que la vitesse v_x(t) s'exprime :
v_x(t) = a \cdot t + v_0 où
v_0 : vitesse initiale du système (m·s-1)
Quant à la coordonnée x(t), celle-ci a pour expression :
x(t) = \dfrac{a}{2} \cdot t^2 + v_0 \cdot t + x_0 où
x_0 : coordonnée initiale du système (m)
Les deux équations horaires précédentes peuvent être déterminées par la recherche de primitives en identifiant les constantes d'intégration à l'aide des conditions initiales du mouvement.
\overrightarrow{\text{OM}}(t) = x(t) \cdot \vec{i}
\vec{v}(t) = v_x(t) \cdot \vec{i} = \dfrac{\text{d}x}{\text{d}t} \cdot \vec{i}
\vec{a}(t) = a_x(t) \cdot \vec{i} = \dfrac{\text{d}v_x}{\text{d}t} \cdot \vec{i} = \dfrac{\text{d}^2x}{\text{d}t^2} \cdot \vec{i}
\vec{v}(t) = v_x(t) \cdot \vec{i} = \dfrac{\text{d}x}{\text{d}t} \cdot \vec{i}
\vec{a}(t) = a_x(t) \cdot \vec{i} = \dfrac{\text{d}v_x}{\text{d}t} \cdot \vec{i} = \dfrac{\text{d}^2x}{\text{d}t^2} \cdot \vec{i}
a. Mouvement rectiligne uniforme
Un mouvement rectiligne est dit uniforme si et seulement si \vec{v} est constant au cours du temps (\vec{v} = \overrightarrow{\text{cste}}).
Ainsi, dans le cas du mouvement rectiligne uniforme, on peut écrire :
\vec{v}(t) = v_x \cdot \vec{i}
Le vecteur accélération \vec{a} d'un mouvement rectiligne uniforme est un vecteur nul :
\vec{a} = \dfrac{\text{d}v_x}{\text{d}t} \cdot \vec{i} = 0 \cdot \vec{i} = \vec{0}
Pour les mouvements rectilignes, la coordonnée x(t) a quant à elle pour forme :
x(t) = v \cdot t + x_0 où
x_0 : coordonnée initiale du système (m)
Cette équation peut être déduite à partir de la recherche d'une primitive de v(t).
➜ .
b. Mouvement rectiligne uniformément accéléré
Un mouvement rectiligne est dit uniformément accéléré si et seulement si \vec{a}(t) est constant au cours du temps :
\vec{a}(t) = a_x \cdot \vec{i}
Cette accélération constante implique que la vitesse v_x(t) s'exprime :
v_x(t) = a \cdot t + v_0 où
v_0 : vitesse initiale du système (m·s-1)
Quant à la coordonnée x(t), celle-ci a pour expression :
x(t) = \dfrac{a}{2} \cdot t^2 + v_0 \cdot t + x_0 où
x_0 : coordonnée initiale du système (m)
Les deux équations horaires précédentes peuvent être déterminées par la recherche de primitives en identifiant les constantes d'intégration à l'aide des conditions initiales du mouvement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 8Mouvement rectiligne uniforme


Sur l'autoroute, le mouvement rectiligne uniforme est très commun, pour des vitesses avoisinant les 130 km·h‑1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 9Mouvement rectiligne uniformément accéléré


Lors des schuss, et pour une durée relativement courte, le mouvement des skieurs peut être considéré comme rectiligne uniformément accéléré.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Attention à ne pas oublier la constante d'intégration lorsque l'on recherche une primitive. C'est en se plaçant dans les conditions initiales du mouvement que l'on détermine sa valeur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 10Exemple de mouvement circulaire uniforme


Plus de 5 500 satellites ont été lancés depuis le début de la conquête spatiale. Destinés à l'espionnage, aux télécommunications, à la géolocalisation, à la météorologie ou à la recherche scientifique, leur mouvement est circulaire uniforme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BMouvements circulaires uniformes
Dans le cas du mouvement circulaire uniforme, quelques simplifications s'opèrent sur les coordonnées de l'accélération dans le repère de Frenet :
Si la norme du vecteur accélération \vec{a}(t) est constante et égale à \dfrac{v^2}{R}, le vecteur \vec{a}(t) ne l'est pas : sa direction change à chaque instant. En effet, \vec{a}(t) étant colinéaire à \overrightarrow{N}, chaque nouvelle position de \text{M} induit une nouvelle direction de \vec{a}(t).
- la composante tangentielle de l'accélération a_\text{T}(t) est nulle, car v(t) = v est constante. On a donc a_\text{T} = 0 m·s-2, ce qui se traduit par une accélération uniquement normale ;
- la composante normale a_\text{N} est constante et égale à a_\text{N} = a = \dfrac{v^2}{R}. \vec{a} et \overrightarrow{N} sont donc colinéaires et de même sens : on parle d'accélération centripète.
Si la norme du vecteur accélération \vec{a}(t) est constante et égale à \dfrac{v^2}{R}, le vecteur \vec{a}(t) ne l'est pas : sa direction change à chaque instant. En effet, \vec{a}(t) étant colinéaire à \overrightarrow{N}, chaque nouvelle position de \text{M} induit une nouvelle direction de \vec{a}(t).
Le vecteur accélération a pour expression, dans le repère de Frenet, pour un mouvement circulaire uniforme :
\vec{a} = a \cdot \overrightarrow{N} = \dfrac{v^2}{R} \cdot \overrightarrow{N} ou
\begin{pmatrix}
0 \\
\dfrac{v^2}{R}
\end{pmatrix}_{(\text{M}, \ \overrightarrow{T}, \ \overrightarrow{N})}
a : accélération centripète (m·s-2)
v : vitesse tangentielle (m·s-1)
R : rayon de la trajectoire circulaire (m)
v : vitesse tangentielle (m·s-1)
R : rayon de la trajectoire circulaire (m)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application
Une voiture à l'arrêt, sur une route plane et horizontale, démarre avec une accélération constante a depuis la position x_0. Déterminer l'équation horaire x(t).
La voiture démarre alors qu'elle est à l'arrêt. On en déduit que la vitesse v(t) s'exprime : v(t) = a \cdot t
La recherche d'une primitive de v(t) conduit à :
Corrigé
La voiture démarre alors qu'elle est à l'arrêt. On en déduit que la vitesse v(t) s'exprime : v(t) = a \cdot t
La recherche d'une primitive de v(t) conduit à :
x(t) = \dfrac{a}{2} \cdot t^2 + x_0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


- Le vecteur vitesse est toujours tangent à la trajectoire pour un mouvement circulaire uniforme ; le vecteur accélération est quant à lui centripète, c'est-à-dire dirigé vers le centre.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

