Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 11
Exercices
Objectif Bac
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29Lancement d'un satellite météorologique
✔ REA/MATH : Intégrer
✔ APP : Faire des prévisions à l'aide d'un modèle
Pour ce lancement, la fusée Ariane 5 a une masse totale m. Sa propulsion est assurée par un ensemble de dispositifs fournissant une force de poussée verticale constante. On étudie le mouvement du système {fusée} dans le référentiel terrestre et on choisit un repère (\text{O}\:,\vec{i}) dans lequel \vec{j} est un vecteur unitaire vertical dirigé vers le haut et porté par l'axe (\text{O}y).
À l'instant t_0 = 0 s, Ariane 5 est immobile. On assimile son étude à celle d'un point M, confondu avec l'origine \text{O} au moment du décollage. La valeur de l'accélération a est donnée par la formule :
Pendant le lancement, on suppose que la valeur de l'accélération reste constante. La trajectoire ascensionnelle de la fusée reste verticale jusqu'à la date t_1 = 6,0 s.
✔ APP : Faire des prévisions à l'aide d'un modèle
D'après le sujet Bac S, Métropole, 2008.
Pour ce lancement, la fusée Ariane 5 a une masse totale m. Sa propulsion est assurée par un ensemble de dispositifs fournissant une force de poussée verticale constante. On étudie le mouvement du système {fusée} dans le référentiel terrestre et on choisit un repère (\text{O}\:,\vec{i}) dans lequel \vec{j} est un vecteur unitaire vertical dirigé vers le haut et porté par l'axe (\text{O}y).
À l'instant t_0 = 0 s, Ariane 5 est immobile. On assimile son étude à celle d'un point M, confondu avec l'origine \text{O} au moment du décollage. La valeur de l'accélération a est donnée par la formule :
M \cdot a = F - M \cdot g
Pendant le lancement, on suppose que la valeur de l'accélération reste constante. La trajectoire ascensionnelle de la fusée reste verticale jusqu'à la date t_1 = 6,0 s.
1. Montrer que a = 6{,}0 m·s-2 et donner le sens du vecteur \vec{a}.
2. Déterminer l'équation horaire de la valeur v(t) de la vitesse.
2. Déterminer l'équation horaire de la valeur v(t) de la vitesse.
3. En déduire l'équation horaire de la valeur y(t) de la position.
4. Déterminer la distance parcourue par la fusée depuis son décollage.
4. Déterminer la distance parcourue par la fusée depuis son décollage.
Données
- Rapport entre l'intensité de la poussée et la masse totale de la fusée : \dfrac{F}{m} = 15{,}8 N·kg-1
- Intensité de pesanteur : g = 9{,}81 N·kg-1
Détails du barème
TOTAL / 5 pts
1 pt
1. Calculer a sans utiliser la calculatrice.
0,5 pt
1. Préciser le sens de a.
1,5 pt
2. Exprimer v(t).
1,5 pt
3. Exprimer y(t).
0,5 pt
4. Calculer l'ascension de la fusée.
➜ Retrouvez plus d'exercices dans le Livret Bac
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Lancer de poids
✔ APP : Faire des prévisions à l'aide d'un modèle
✔ COM : Rédiger correctement une résolution d'exercice
✔ COM : Rédiger correctement une résolution d'exercice
D'après le sujet Bac S, Nouvelle-Calédonie, 2004.
Lors des Championnats du monde d'athlétisme qui ont eu lieu à Paris en août 2003, le vainqueur de l'épreuve du lancer du poids, Andrei Mikhnevich, a réussi un jet à une distance d = 21{,}69 m.
L'entraîneur de l'un de ses concurrents souhaite étudier ce lancer. Pour cela, il dispose pour le centre d'inertie du boulet, en plus de la valeur 21,69 m du record, de la vitesse initiale v_0 mesurée à l'aide d'un cinémomètre et de l'altitude h.
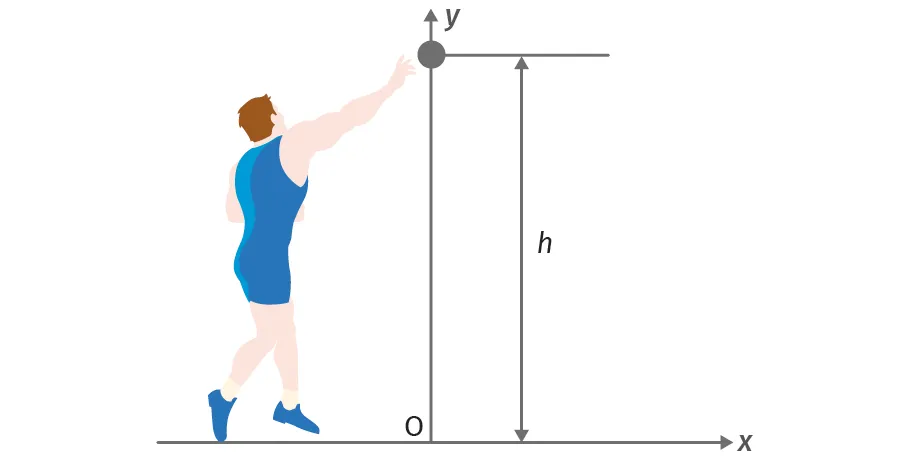
L'entraîneur de l'un de ses concurrents souhaite étudier ce lancer. Pour cela, il dispose pour le centre d'inertie du boulet, en plus de la valeur 21,69 m du record, de la vitesse initiale v_0 mesurée à l'aide d'un cinémomètre et de l'altitude h.
Le zoom est accessible dans la version Premium.
L'entraîneur a étudié le mouvement du boulet et a obtenu trois graphes :
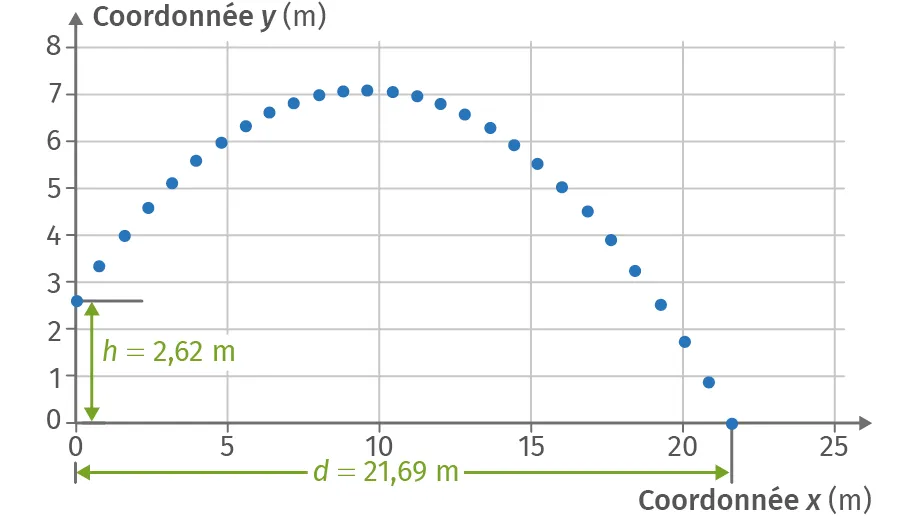
- le graphe de la trajectoire y = f(x) du boulet ;
Le zoom est accessible dans la version Premium.
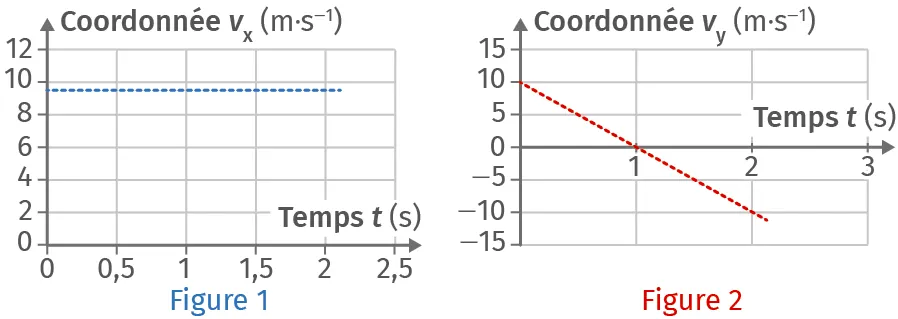
- les graphes de v_x(t) et de v_y(t) en fonction du temps t où v_x(t) et v_y(t) sont les coordonnées horizontale et verticale du vecteur vitesse \vec{v}(t).
Données
- Vitesse initiale du boulet : v_0 = 13{,}8 m⋅s-1
- Hauteur initiale du lancer : h = 2{,}62 m
- Intensité de pesanteur : g = 9{,}81 N⋅kg-1
Le zoom est accessible dans la version Premium.
I. Étude de la projection horizontale du mouvement
du boulet
1. Déterminer la composante v_{0x} du vecteur vitesse du boulet à l'instant de date t_0 = 0 s
2. Caractériser la nature du mouvement de la projection sur l'axe (\text{O}x) en justifiant la réponse.
3. Déterminer la composante v_{\text{S}x} du vecteur vitesse lorsque le boulet est au sommet S de sa trajectoire.
II. Étude des conditions initiales du lancer
1. En utilisant la figure 2, déterminer la composante v_{0y} du vecteur vitesse à l'instant t_0 = 0 s.
2. À partir des résultats précédents, vérifier que la valeur de la vitesse initiale et celle de l'angle de tir soient compatibles avec les valeurs respectives v_0 = 13{,}8 m·s–1 et \alpha = 43°.
III. Étude du vecteur vitesse du boulet
1. Déterminer toutes les caractéristiques du vecteur vitesse du boulet au sommet de la trajectoire.
2. Reproduire, à main levée et sans souci d'échelle, le graphe y = f(x), puis représenter :
1. Déterminer la composante v_{0x} du vecteur vitesse du boulet à l'instant de date t_0 = 0 s
2. Caractériser la nature du mouvement de la projection sur l'axe (\text{O}x) en justifiant la réponse.
3. Déterminer la composante v_{\text{S}x} du vecteur vitesse lorsque le boulet est au sommet S de sa trajectoire.
II. Étude des conditions initiales du lancer
1. En utilisant la figure 2, déterminer la composante v_{0y} du vecteur vitesse à l'instant t_0 = 0 s.
2. À partir des résultats précédents, vérifier que la valeur de la vitesse initiale et celle de l'angle de tir soient compatibles avec les valeurs respectives v_0 = 13{,}8 m·s–1 et \alpha = 43°.
III. Étude du vecteur vitesse du boulet
1. Déterminer toutes les caractéristiques du vecteur vitesse du boulet au sommet de la trajectoire.
2. Reproduire, à main levée et sans souci d'échelle, le graphe y = f(x), puis représenter :
- le vecteur vitesse du boulet à l'instant du lancer ;
- le vecteur vitesse du boulet au sommet de la trajectoire.
Cette fonctionnalité est accessible dans la version Premium.
IV. Étude théorique du mouvement
L'accélération du boulet admet comme coordonnées en fonction du temps :
1. Dans le repère d'espace défini en introduction, montrer que les équations horaires de la vitesse s'expriment sous la forme :
2. Dans le repère d'espace défini en introduction, montrer que les équations horaires du mouvement s'expriment sous la forme :
x(t) = v_0 \cdot \cos(\alpha) \cdot t
y(t) = - \dfrac{1}{2}g \cdot t^2 + v_0 \cdot \sin(\alpha) \cdot t + h
L'équation de la trajectoire y(x) s'obtient en isolant t dans l'équation horaire x(t), puis en remplaçant t par sa nouvelle forme dans l'équation horaire y(t).
3. Vérifier ainsi que l'équation de la trajectoire est de la forme :
4. En déduire la position théorique atteinte par le boulet lorsqu'il touche le sol avec les conditions initiales précédemment évoquées : v_0 = 13{,}8 m·s–1, h = 2{,}62 m et \alpha = 43°.
V. Amélioration des performances du lancer
L'entraîneur veut ensuite savoir sur quel(s) paramètre(s) il peut travailler pour améliorer la performance de l'athlète. L'entraîneur décide donc d'étudier l'influence de la valeur v_0 de la vitesse initiale du lancer et de l'angle de tir \alpha. Il réalise des séries de simulations rassemblées dans les réseaux de courbes correspondants aux graphiques suivants :
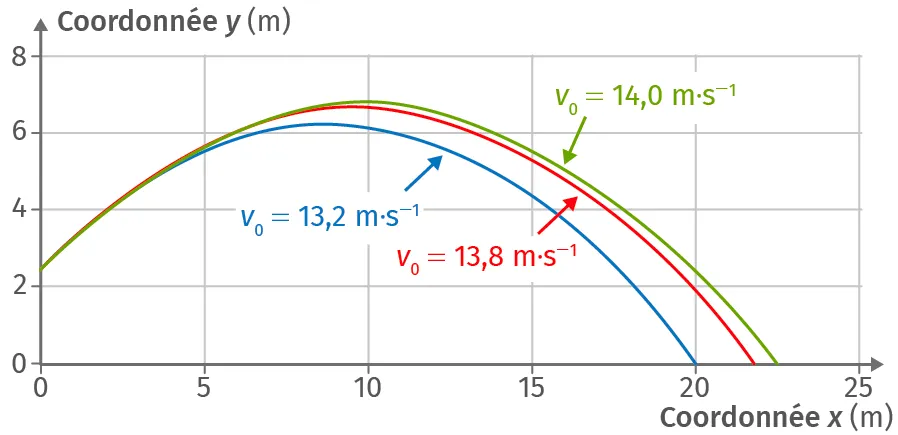
L'angle de tir est maintenu constant, soit \alpha = 41 °.
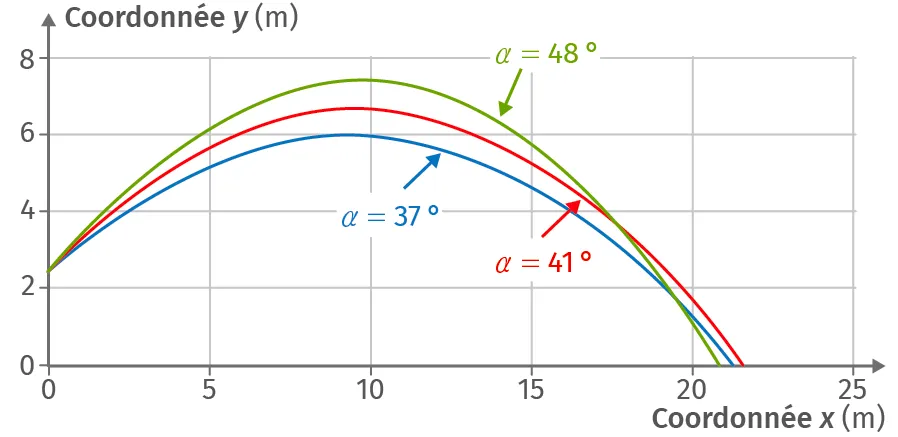
La vitesse est maintenue constante, soit v_0 = 13{,}8 m·s–1
Confronter les graphiques précédents pour en déduire si, parmi les combinaisons proposées, il en existe une satisfaisante pour battre le record du monde. Justifier la réponse.
L'accélération du boulet admet comme coordonnées en fonction du temps :
\vec{a}(t)
\bigg(\begin{array}{l}
a_x(t) = 0 \\
a_y(t) = -g
\end{array}\bigg)_{(\text{O}, \ \overrightarrow{i}, \ \overrightarrow{j})}
1. Dans le repère d'espace défini en introduction, montrer que les équations horaires de la vitesse s'expriment sous la forme :
\vec{v}(t)
\bigg(\begin{array}{l}
v_x(t) = v_0 \cdot \cos(\alpha) \\
v_y(t) = -g \cdot t + v_0 \cdot \sin(\alpha)
\end{array}\bigg)_{(\text{O}, \ \overrightarrow{i}, \ \overrightarrow{j})}
v_0 : vitesse initiale du jet (m·s-1)
\alpha : l'angle de tir (°)
\alpha : l'angle de tir (°)
2. Dans le repère d'espace défini en introduction, montrer que les équations horaires du mouvement s'expriment sous la forme :
x(t) = v_0 \cdot \cos(\alpha) \cdot t
y(t) = - \dfrac{1}{2}g \cdot t^2 + v_0 \cdot \sin(\alpha) \cdot t + h
L'équation de la trajectoire y(x) s'obtient en isolant t dans l'équation horaire x(t), puis en remplaçant t par sa nouvelle forme dans l'équation horaire y(t).
3. Vérifier ainsi que l'équation de la trajectoire est de la forme :
y(x) = - \dfrac{g \cdot x^2}{2\ v_0^2 \cdot \cos(\alpha)^2} + \tan(\alpha) \cdot x + h
4. En déduire la position théorique atteinte par le boulet lorsqu'il touche le sol avec les conditions initiales précédemment évoquées : v_0 = 13{,}8 m·s–1, h = 2{,}62 m et \alpha = 43°.
V. Amélioration des performances du lancer
L'entraîneur veut ensuite savoir sur quel(s) paramètre(s) il peut travailler pour améliorer la performance de l'athlète. L'entraîneur décide donc d'étudier l'influence de la valeur v_0 de la vitesse initiale du lancer et de l'angle de tir \alpha. Il réalise des séries de simulations rassemblées dans les réseaux de courbes correspondants aux graphiques suivants :
Le zoom est accessible dans la version Premium.
L'angle de tir est maintenu constant, soit \alpha = 41 °.
Le zoom est accessible dans la version Premium.
La vitesse est maintenue constante, soit v_0 = 13{,}8 m·s–1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASaut à la perche
✔ APP : Extraire l'information utile
D'après le sujet Bac S, Antilles, 2019.
Le zoom est accessible dans la version Premium.
Le saut à la perche est un sport d'athlétisme faisant partie des dix épreuves du décathlon. Il est présent aux Jeux Olympiques depuis 1896 pour les hommes, et 2000 pour les femmes. Le saut se déroule en trois phases : prise d'élan, phase ascendante et phase descendante.
Lors de la prise d'élan, le perchiste doit atteindre une vitesse maximale au moment de l'impulsion. S'il l'atteint trop tôt, il risque de ne pas pouvoir la conserver jusqu'à l'impulsion. Pour éviter cela, ce n'est que dans les derniers mètres de la prise d'élan qu'il redouble d'efforts pour atteindre sa vitesse maximale.
Le zoom est accessible dans la version Premium.
1. Comment peut‑on qualifier le mouvement du perchiste entre 3 s et 4 s ? Relever la vitesse du perchiste.
2. Même question entre 5 s et 7 s.
3. Calculer l'accélération du perchiste entre 5 s et 7 s.
2. Même question entre 5 s et 7 s.
3. Calculer l'accélération du perchiste entre 5 s et 7 s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCanon de Paris
✔ VAL : Analyser des résultats
Le canon de Paris est l'un des canons les plus célèbres dans l'histoire de l'artillerie. Il a servi à bombarder Paris à la fin de la Première Guerre mondiale. La longueur (36 m) et la masse (100 t) du tube du canon étaient si importantes que les ingénieurs allemands ont dû mettre au point un système de soutènement inédit en artillerie composé de haubans et d'un mât central, comme pour un pont suspendu.
D'après le sujet Bac S, Amérique du Sud, 2019.
Le canon de Paris est l'un des canons les plus célèbres dans l'histoire de l'artillerie. Il a servi à bombarder Paris à la fin de la Première Guerre mondiale. La longueur (36 m) et la masse (100 t) du tube du canon étaient si importantes que les ingénieurs allemands ont dû mettre au point un système de soutènement inédit en artillerie composé de haubans et d'un mât central, comme pour un pont suspendu.
L'obus est propulsé dans la haute atmosphère, où les frottements de l'air sont moindres, avec une élévation égale à 50°. Lors des essais finaux de janvier 1918, le canon tira un obus de 105 kg avec une vitesse de 1 600 m·s-1. Le vol de l'obus a duré 176 s et le point d'impact était à 126 km de distance. Au plus haut de sa trajectoire, l'obus était à 42 km d'altitude, soit la plus haute altitude jamais atteinte à l'époque.
Le zoom est accessible dans la version Premium.
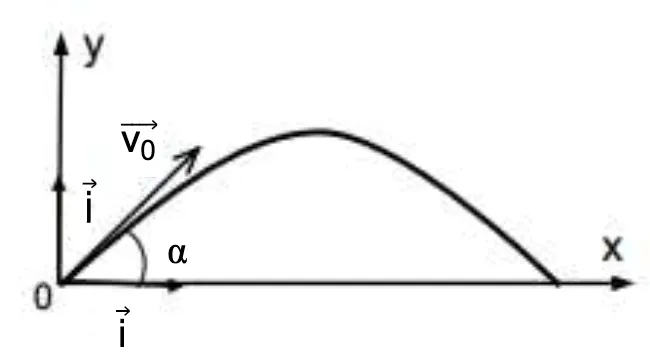
On étudie le mouvement de l'obus dans le repère (x \mathrm{O} y) (voir le schéma ci‑dessus). Le point O correspond à la sortie du tube du canon. L'angle \alpha entre le tube du canon et le sol correspond à l'élévation citée en introduction. \overrightarrow{v_0} est le vecteur vitesse au moment de l'éjection. Le vecteur accélération est égal à \vec{a} = -g \cdot \vec{j}.
1. Déterminer les expressions de v_x(t) et de v_y(t) puis en déduire les équations horaires du mouvement :
x = v_0 \cdot \cos(\alpha ) \cdot t
y(t) = -\dfrac{1}{2} \ g \cdot t^2 + v_0 \cdot \sin(\alpha ) \cdot t
2. Déterminer l'équation de la trajectoire.
Dans les questions qui suivent, on cherche à vérifier les valeurs données concernant la portée, la durée de vol et l'altitude maximale. On néglige la longueur du tube du canon et on suppose que l'impact se fait à la même altitude que l'éjection.
3. Justifier que l'on peut négliger la longueur du tube.
x = v_0 \cdot \cos(\alpha ) \cdot t
y(t) = -\dfrac{1}{2} \ g \cdot t^2 + v_0 \cdot \sin(\alpha ) \cdot t
2. Déterminer l'équation de la trajectoire.
Dans les questions qui suivent, on cherche à vérifier les valeurs données concernant la portée, la durée de vol et l'altitude maximale. On néglige la longueur du tube du canon et on suppose que l'impact se fait à la même altitude que l'éjection.
3. Justifier que l'on peut négliger la longueur du tube.
4. En utilisant l'équation établie à la question 2, calculer la portée théorique (distance entre le point d'impact et le canon).
5. En utilisant l'équation établie à la question 2, calculer l'altitude maximale théorique.
6. En utilisant l'équation établie à la question 1, calculer la durée du vol.
5. En utilisant l'équation établie à la question 2, calculer l'altitude maximale théorique.
6. En utilisant l'équation établie à la question 1, calculer la durée du vol.
Données
- Intensité de pesanteur : g = 9{,}81 N·kg-1
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah