Physique-Chimie Terminale Spécialité
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 21
Cours
Évolutions temporelles dans un circuit capacitif
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Modélisation d'un condensateur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
APrincipe et utilisation des condensateurs
Un condensateur est un dipôle électrique constitué de deux plaques conductrices très proches l'une de l'autre et séparées par un isolant.
Alimenté par un courant électrique continu, des charges de signe opposé s'accumulent sur les plaques. Ce phénomène est appelé effet capacitif. Le condensateur est utilisé principalement pour :
- stabiliser une alimentation électrique
- traiter des signaux périodiques en séparant par exemple le courant alternatif du courant continu
- stocker de l'énergie, auquel cas on parle de supercondensateur
Les condensateurs peuvent aussi être utilisés dans différents capteurs, comme les microphones (doc. 2). Ils sont aussi utilisés dans des circuits électriques alimentant les tubes à décharge.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Schéma d'un condensateur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Microphone
Des condensateurs sont utilisés dans la fabrication de microphones.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCapacité d'un condensateur
Expérimentalement, on observe que la charge totale Q sur une plaque du condensateur est proportionnelle à la tension u_{\mathrm{C}} aux bornes de ce condensateur.
La capacité C, exprimée en farad (F), d'un condensateur est définie comme le coefficient de proportionnalité entre la charge Q
et la tension u_{\mathrm{C}} :
Q=C · u_{\mathrm{C}}
C : capacité du condensateur (F)
u_{\mathrm{C}} : tension aux bornes du condensateur (V)
u_{\mathrm{C}} : tension aux bornes du condensateur (V)
Son ordre de grandeur usuel est compris entre 1 nF et 1 mF. La capacité C dépend de plusieurs paramètres comme la distance entre les armatures, leur surface, la géométrie générale du condensateur ou encore la nature du matériau séparant les deux plaques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Capacité
Capacité : coefficient de proportionnalité entre la charge Q portée par les armatures du condensateur et la tension u_{\mathrm{c}} à ses bornes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'électrosphère (couche atmosphérique ionisée) et le sol de la Terre forment un gigantesque condensateur sphérique terrestre d'une capacité proche de 50 mF.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLien entre tension et intensité
L'intensité électrique I traversant un circuit correspond au débit de charges électriques :
i=\frac{\mathrm{d} Q}{\mathrm{d} t}
i : intensité du courant (A)
Q : charge électrique accumulée (C)
t : temps (s)
Q : charge électrique accumulée (C)
t : temps (s)
En remplaçant Q avec la relation précédente, on obtient alors :
i=C · \frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}
Cette relation caractérise le comportement d'un condensateur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Charge d'un condensateur d'un
circuit RC en série
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASchéma électrique du circuit RC
Soit la charge d'un condensateur initialement déchargé dans le circuit schématisé ci‑dessous :
En fermant l'interrupteur à t = 0 s, la charge du condensateur commence. La tension u_{\mathrm{C}} augmente alors au cours du temps.
En fermant l'interrupteur à t = 0 s, la charge du condensateur commence. La tension u_{\mathrm{C}} augmente alors au cours du temps.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Condensateur chargé
Condensateur déchargé
Condensateur chargé :
le condensateur est chargé lorsque la tension à ses bornes atteint sa valeur maximale.
Condensateur déchargé :
le condensateur est déchargé lorsque la tension à ses bornes est nulle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Attention, le résistor et le condensateur sont en convention récepteur.
- Il est nécessaire de diviser par R·C pour mettre l'équation sous la forme habituelle avec chaque terme en (V·s-1).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BMise en équation du circuit
L'objectif est de trouver la tension u_{\mathrm{C}} au cours du temps durant la charge du condensateur, celui‑ci étant initialement déchargé.
Selon la loi des mailles :
u_{\mathrm{C}}+u_{\mathrm{R}}=E
u_{\mathrm{C}}+R · i=E
u_{\mathrm{C}}+R · C · \frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}=E
\frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}+\frac{u_{\mathrm{C}}}{R · C}=\frac{E}{R · C}
u_{\mathrm{C}}+u_{\mathrm{R}}=E
u_{\mathrm{C}}+R · i=E
u_{\mathrm{C}}+R · C · \frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}=E
\frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}+\frac{u_{\mathrm{C}}}{R · C}=\frac{E}{R · C}
On obtient une équation différentielle du premier ordre en u_{\mathrm{C}}. La résolution de cette équation aboutit à :
u_{\mathrm{C}}(t)=E ·\left(1-\exp \left(-\frac{t}{R \cdot C}\right)\right)
Le régime transitoire est le régime pendant lequel le condensateur se charge. Lorsque la tension u_{\mathrm{C}} atteint sa valeur maximale constante, on parle de régime permanent ().
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Courbe de charge \boldsymbol{u_{\mathbf{C}}=f(t)}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4Capacité
La capacité C du condensateur dépend de la géométrie et du matériau isolant utilisé entre les armatures. Pour un condensateur plan :
C=\varepsilon · \frac{S}{e}
C : capacité du condensateur (F)
ε : coefficient lié à la nature du matériau séparant les armatures (F·m-1)
S : surface des armatures (m2)
e : distance séparant les armatures (m)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CTemps caractéristique de charge
Dans le cadre d'une fonction exponentielle de la forme f(t)=\exp \left(-\frac{t}{\tau}\right), on définit \tau comme le temps caractéristique. On adopte cette définition pour le temps caractéristique de charge d'un condensateur.
Par identification u_{\mathrm{C}}(t), le temps caractéristique s'exprime :
L'expression de u_{\mathrm{C}}(t) devient donc :
\tau=R \cdot C
L'expression de u_{\mathrm{C}}(t) devient donc :
u_{\mathrm{C}}(t)=E \cdot\left(1-\exp \left(-\frac{t}{\tau}\right)\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le temps caractéristique n'est pas le temps qu'il faut au condensateur pour se charger complètement : au bout de t = τ, le condensateur n'est chargé qu'à 63 %. Le condensateur n'est généralement considéré chargé qu'au bout de 5 τ environ (chargé à 99 %).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Décharge d'un condensateur d'un circuit RC série
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASchéma électrique du circuit RC
Un condensateur initialement chargé avec une tension E peut se décharger dans un dipôle, comme une résistance par exemple.
On ferme l'interrupteur K à t = 0 s. Le condensateur commence à se décharger dans la résistance.
On ferme l'interrupteur K à t = 0 s. Le condensateur commence à se décharger dans la résistance.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Attention, lors de la décharge, le courant circule physiquement toujours à l'extérieur du condensateur en partant de l'armature chargée positivement du condensateur vers l'armature chargée négativement.
- Il est nécessaire de diviser par R · C pour mettre l'équation sous la forme que l'on sait résoudre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5Courbe de décharge
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BMise en équation du circuit
Comme précédemment, il faut déterminer la tension u_{\mathrm{C}}(t) au cours du temps. L'interrupteur K est fermé à t = 0 s.
Selon la loi des mailles :
u_{\mathrm{C}}+u_{\mathrm{R}}=0
u_{\mathrm{C}}+R · i=0
u_{\mathrm{C}}+R · C · \frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}=0
\frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}+\frac{u_{\mathrm{C}}}{R · C}=0
On obtient à nouveau une équation différentielle du premier ordre en u_{\mathrm{C}}. En la résolvant :
u_{\mathrm{C}}+u_{\mathrm{R}}=0
u_{\mathrm{C}}+R · i=0
u_{\mathrm{C}}+R · C · \frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}=0
\frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}+\frac{u_{\mathrm{C}}}{R · C}=0
On obtient à nouveau une équation différentielle du premier ordre en u_{\mathrm{C}}. En la résolvant :
u_{\mathrm{C}}(t)=E ·\exp \left(-\frac{t}{R ·C}\right)
Le régime durant lequel le condensateur se décharge est appelé régime transitoire. Lorsque la tension atteint la valeur nulle, on est en régime permanent.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 6Bouteille de Leyde (1745)
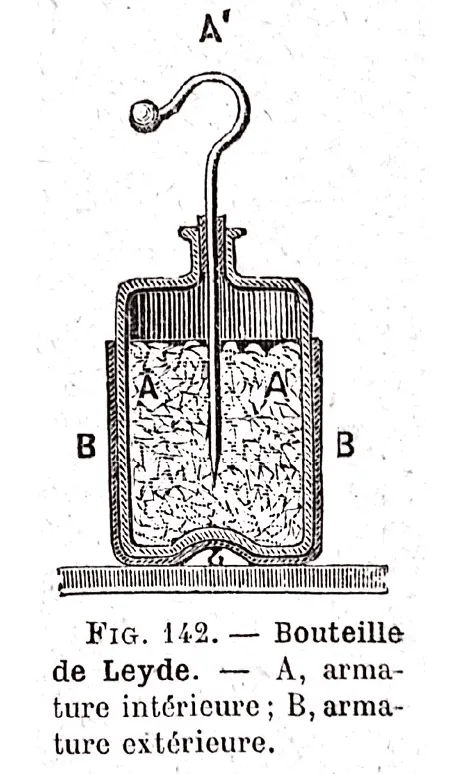
À Versailles, l'expérience de la décharge d'une grosse bouteille de Leyde à travers le circuit formé fut présentée à Louis XV et à plus de deux cents courtisans. La décharge brusque de ce premier condensateur fit sursauter toute la cour.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CTemps caractéristique de décharge
La même définition s'applique ici que lors de la charge.
Par identification, le temps caractéristique \tau vaut :
\tau=R · C
La solution de l'équation différentielle s'exprime alors en fonction de \tau :
u_{\mathrm{C}}(t)=E · \exp \left(-\frac{t}{\tau}\right)
La charge et la décharge du condensateur s'effectuent avec un temps caractéristique identique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Comme pour la charge, ce temps caractéristique n'est pas le temps de décharge. Au bout de t = τ, le condensateur n'est déchargé qu'à 37 %. Le condensateur est considéré déchargé qu'au bout de 5 τ environ (soit une décharge jusqu'à 1 %).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Capteurs capacitifs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
APrésentation
L'effet capacitif est utilisé dans de nombreux capteurs afin de mesurer différentes grandeurs physiques.
Pour cela, la grandeur physique que l'expérimentateur souhaite mesurer doit être reliée à la valeur de la capacité C du capteur.
Exemple :
Lorsqu'un doigt conducteur électrique touche un écran, il y a transfert de charges. Des capteurs capacitifs détectent cette différence de charge afin de connaître la position du doigt.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 7Écran capacitif
Lors d'un contact avec un doigt, l'écran tactile se décharge localement. Cet effet permet de repérer la position du contact.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BExemples de capteurs capacitifs à effet mécanique
Le déplacement d'une des électrodes par rapport à l'autre modifie la capacité du condensateur.
Exemple :
- Les capteurs de pression ou de déplacement sont constitués d'une armature mobile et d'une armature fixe permettant de repérer une variation de capacité due à une variation de distance entre les électrodes (microphones).
- L'accéléromètre utilise en général deux capteurs capacitifs de déplacement qui mesurent le déplacement d'un objet par rapport à un support (vibromètre à ondes sismiques, manette).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Capteur capacitif
Capteur capacitif : appareil utilisant un condensateur et l'effet capacitif pour mesurer une grandeur physique, comme une masse, un déplacement ou une force par exemple.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Attention, les capteurs ne mesurent pas directement la grandeur physique : un étalonnage permet de relier la capacité C à la grandeur souhaitée. Cet étalonnage permet ensuite de déterminer la grandeur physique voulue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CExemples de capteurs capacitifs liés aux caractéristiques de l'isolant
La modification des caractéristiques du milieu entre les électrodes modifie la capacité du condensateur.
Exemple :
- Les capteurs d'humidité ou de température par détection d'une variation des caractéristiques de l'isolant (comme une céramique) entre les électrodes.
- Les capteurs de proximité : si un objet s'approche de l'extrémité du capteur, la valeur de C est modifiée (contrôle de remplissage dans des flacons ou des cuves opaques).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 8Capteur de la Wiimote
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
