✔ VAL : Faire preuve d'esprit critique

Une pile alcaline, tout comme une pile saline, fonctionne à partir des mêmes couples. En revanche, une pile alcaline utilise de l'hydroxyde de potassium \text{(K}^+\text{(aq) ; HO}^-\text{(aq))} comme électrolyte alors qu'une pile saline utilise du chlorure d'ammonium \left(\mathrm{NH}_{4}^{+}(\mathrm{aq}) ; \mathrm{Cl}^{-}(\mathrm{aq})\right) et du chlorure de zinc \left(\mathrm{Zn}^{2+}(\mathrm{aq}) ; 2 \mathrm{Cl}^{-}(\mathrm{aq})\right).
La solution alcaline permet aux ions de circuler plus vite que dans un mélange de chlorure d'ammonium et de chlorure de zinc.
Les piles salines ne fournissent que de faibles intensités.

1. Expliquer pourquoi les piles alcalines peuvent fournir des intensités plus élevées.

2. Choisir le type de pile pour alimenter :
a. une télécommande.

b. un petit moteur.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23
Pile argent‑zinc

✔ RAI/ANA : Construire un raisonnement

Une pile possède une anode en zinc \text{Zn(s)}, dans une solution d'ions zinc \text{Zn}^{2+}\text{(aq)} et une cathode en argent \text{Ag(s)} dans une solution d'ions argent \text{Ag}^+\text{(aq)}.

1. Écrire les demi‑équations d'oxydoréduction ayant lieu aux électrodes.

2. En déduire l'équation de fonctionnement de la pile.

3. En déduire la quantité de matière d'électrons échangés.

4. Calculer la capacité électrique sachant qu'elle s'épuise après avoir oxydé m = 5{,}0 g de zinc.

5. Calculer sa durée de fonctionnement pour un courant d'intensité constante I = 10 mA.

Données

Couples d'oxydoréduction : \mathrm{Ag}^{+}(\mathrm{aq}) / \mathrm{Ag}(\mathrm{s}) \text { et } \mathrm{Zn}^{2+}(\mathrm{aq}) / \mathrm{Zn}(\mathrm{s})
Masse molaire du zinc : M\text{(Zn)} = 65{,}4 g⋅mol^-1

Détails du barème
TOTAL /6 pts

0,5 pt

1. Écrire les demi‑équations.

1 pt

2. Établir l'équation de réaction de la pile.

0,5 pt

3. Déterminer un nombre d'électrons échangés.

2 pt

4. Exploiter Q_\text{max} = n_\text{e} ⋅ F

2 pts

5. Exploiter Q_\text{max} = I ⋅ Δt

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

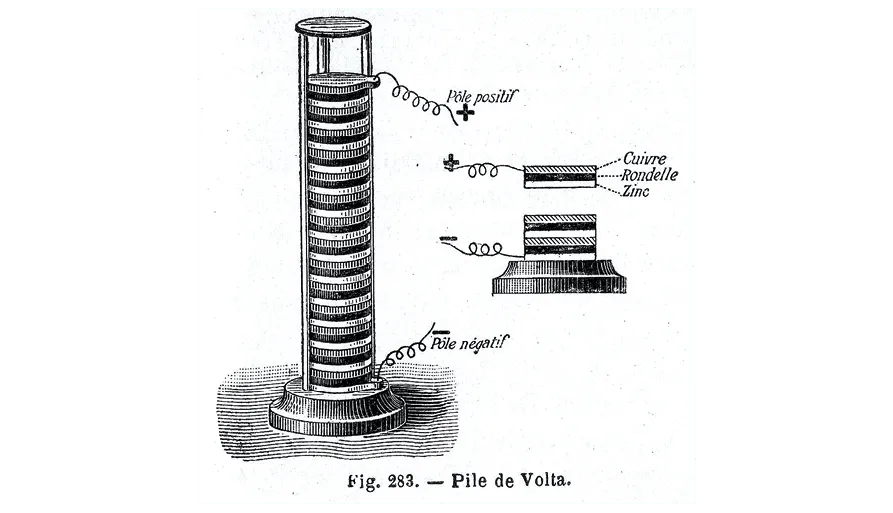
24
Pile de Volta

✔ RAI/MOD : Modéliser une transformation

La pile de Volta fait intervenir les couples \text{Zn}^{2+}\text{(aq)/Zn(s)} et \text{H}^+\text{(aq)/H}_2\text{(g)}. Le zinc \text{Zn(s)} est oxydé, l'eau est réduite.

1. Écrire les demi‑équations des deux couples oxydant‑réducteur.

2. En déduire l'équation de fonctionnement de la pile de Volta.

Schéma de la pile voltaïque inventée par Volta : une colonne de disques de cuivre et de zinc, séparés par du carton imbibé d'eau salée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

25
Caractéristique d'une pile

✔ VAL : Analyser des résultats

La caractéristique courant‑tension d'une pile est une droite affine.

1. Déterminer la tension à vide E de la pile.

2. Calculer la résistance interne r de la pile.

3. Lorsque la pile atteint l'équilibre, elle est usée et ne fonctionne plus. Considérant une pile dont la capacité électrique est Q_\text{max} = 500 C, calculer la quantité de matière d'électrons échangés pendant toute sa durée de fonctionnement.

4. Déterminer la durée de fonctionnement de la pile en considérant un courant constant d'intensité I = 10 mA.

Données

Constante de Faraday : F = 9{,}65 \times 10^4 C⋅mol^-1

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
Vitamine C

✔ REA : Appliquer une formule

L'acide ascorbique \text{C}_6\text{H}_8\text{O}_6, dont l'énantiomère L‑ascorbique est connu sous le nom de vitamine C, réagit avec l'eau selon l'équation suivante :

\mathrm{C}_{6} \mathrm{H}_{8} \mathrm{O}_{6}(\mathrm{aq})+\mathrm{H}_{2} \mathrm{O}(\mathrm{l}) \rightleftarrows \mathrm{C}_{6} \mathrm{H}_{7} \mathrm{O}_{6}^{-}(\mathrm{aq})+\mathrm{H}_{3} \mathrm{O}^{+}(\mathrm{aq})

La constante d'équilibre de la réaction est égale à K = 7{,}9 \times 10^{-5}.

1. Préciser la nature de la réaction.

Un comprimé contenant 3{,}0 \times 10^{-3} mol de vitamine C est dissous dans 200 mL d'eau contenant déjà des ions \mathrm{C}_{6} \mathrm{H}_{7} \mathrm{O}_{6}^{-}(\mathrm{aq}) à la concentration \left[\mathrm{C}_{6} \mathrm{H}_{7} \mathrm{O}_{6}^{-}\right]_{\mathrm{i}}=0{,}10 mol⋅L^-1

2. Avant réaction, déterminer la concentration initiale d'acide ascorbique \text{C}_6\text{H}_8\text{O}_6\text{(aq)}.

3. En déduire le sens d'évolution spontanée de cette réaction.

Données

\text{pH} de la solution avant dissolution du comprimé : \text{pH} = 7{,}8

Doc.
Teneur en vitamine C de plusieurs aliments

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
Question de taille

✔ VAL : Faire preuve d'esprit critique

L'équation de la réaction d'une pile cuivre‑zinc est :

\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \rightleftarrows \mathrm{Cu}(\mathrm{s})+\mathrm{Zn}^{2+}(\mathrm{aq})

La lame de zinc constitue l'anode.

1. Écrire les demi‑équations associées.

2. Exprimer la quantité de matière d'électrons transférés.

3. Calculer la capacité électrique de cette pile.

4. Les masses de chaque électrode sont doublées.
Calculer la nouvelle capacité électrique.

5. Conclure quant à l'influence de la masse de l'anode et de la cathode.

Données

Masses des électrodes : m_\text{anode} = 8{,}0 g et m_\text{cathode} = 6{,}0 g
Constante de Faraday : F = 9{,}65 \times 10^4 C⋅mol^-1
Masses molaires : M(\text{Zn}) = 65,4 g·mol^-1 et M(\text{Cu}) = 63,5 g·mol^-1

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28
Piles qui chauffent

✔ RAI/ANA : Construire un raisonnement

Bande dessinée: Gaston Lagaffe sur le verglas. Il explique son invention pour faire fondre la glace avec des piles et résistances dans ses chaussures.

1. Rappeler quel phénomène est mis en jeu.

2. Gaston utilise deux piles, une dans chaque chaussure, dont la tension à vide vaut 12 \text{V}. Le courant circule avec une intensité I = 0{,}50 A. Calculer la puissance dissipée P.

3. En déduire l'énergie dissipée au bout de 10 min.

4. Déterminer la durée maximale de promenade de Gaston avec ses chaussures sachant que la capacité électrique de chaque pile vaut Q_\text{max} = 4 320 C.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29

Copie d'élève à commenter

Proposer une justification pour chaque erreur relevée par le correcteur.

L'équation de fonctionnement de la pile cuivre‑zinc est :

\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \rightleftarrows \mathrm{Zn}^{2+}(\mathrm{aq})+\mathrm{Cu}(\mathrm{s})

La constante d'équilibre de cette réaction est égale à K = 1{,}9 \times 10^{37}.

1. Écrire l'expression littérale du quotient de réaction Q_\text{r}.

L'expression littérale de Q_\text{r} = \frac{\left[\mathrm{Zn}^{2+}\right]}{\left[\mathrm{Cu}^{2+}\right]} car le cuivre et le zinc étant solides, on considère que \color{red}\cancel{\color{black}\text{[Zn] = [Cu]} = 0}.

2. Calculer ce quotient à l'instant initial sachant que \left[\mathrm{Cu}^{2+}\right]_{\mathrm{i}}=3{,}0 \times 10^{-2} mol⋅L^-1 et \left[\mathrm{Zn}^{2+}\right]_{\mathrm{i}}=7{,}0 \times 10^{-2} mol⋅L^-1.

AN : Q_\text{r,i} = \frac{7{,}0 \times 10^{-2}}{3{,}0 \times 10^{-2}} = 2{,}3 ~~mol~~

3. Déterminer le sens d'évolution spontanée de cette réaction.

Ici Q_\text{r,i} \lt K, donc la réaction évolue dans le sens ~~indirect~~.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30
Générateur d'électricité

✔ REA : Appliquer une formule

Une pile électrique échange une quantité de matière d'électrons n_\text{e} = 0{,}30 mol en débitant un courant d'intensité supposée constante I = 50 mA.

1. Exprimer puis calculer la capacité électrique de la pile.

2. En déduire la durée de fonctionnement.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31
Dosage et durée de fonctionnement

✔ RAI/ANA : Construire un raisonnement

D'après le sujet Bac S, Polynésie, 2012.

Une pile diiode‑zinc débite un courant d'intensité supposée constante I = 50 mA pendant une durée Δt. La lame de platine baigne dans une solution de diiode \text{I}_2\text{(aq)} et d'ions iodure \text{I}^-\text{(aq)}. Pour déterminer la quantité de \text{I}_2 \text{(aq)} restant en solution, on réalise un dosage avec une solution de concentration c = 2{,}0 \times 10^{-1} mol⋅L^-1 en ion thiosulfate \mathrm{S}_{2} \mathrm{O}_{3}^{2-}(\mathrm{aq}). Le volume versé à l'équivalence est V_\text{E} = 14{,}7 mL. La réaction support du dosage est :

2 \mathrm{S}_{2} \mathrm{O}_{3}^{2-}(\mathrm{aq})+\mathrm{I}_{2}(\mathrm{aq}) \rightarrow \mathrm{S}_{4} \mathrm{O}_{6}^{2-}(\mathrm{aq})+2 \mathrm{I}^{-}(\mathrm{aq})

1. Déterminer la quantité de matière de diiode, notée n\text{(I}_2), présente dans l'électrolyte.

Initialement, la quantité de matière de diiode est égale à n\text{(I}_2)_\text{i} = 1{,}00 \times 10^{-2} mol.

2. En déduire la quantité de matière n\text{(I}_2)_\text{cons} consommée pendant la durée de fonctionnement de la pile \Delta t.

3. Vérifier que la capacité électrique Q_\text{max} fournie par la pile est proche de 1{,}6 \times 10^3 C.

4. En déduire la durée de fonctionnement \Delta t de la pile.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

32
Sens d'évolution d'une pile

✔ RAI/MOD : Modéliser une transformation

Le zinc réagit avec l'argent selon la réaction :

\mathrm{Zn}(\mathrm{s})+2 \mathrm{Ag}^{+}(\mathrm{aq}) \rightleftarrows \mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{Ag}(\mathrm{s})

La constante d'équilibre de cette réaction est K = 10^{52}.

1. Donner l'expression du quotient de réaction Q_\text{r}.

2. Calculer la valeur de Q_\text{r} à l'état initial et en déduire le sens d'évolution spontanée d'une pile zinc‑argent dont les électrodes en argent et en zinc baigne dans des électrolytes de concentration initiale \left[\mathrm{Ag}^{+}\right]_{\mathrm{i}}=\left[\mathrm{Zn}^{2+}\right]_{\mathrm{i}}=0,2 mol·L^-1.

3. Identifier l'anode et la cathode.

4. Faire un schéma légendé de la pile zinc‑argent et indiquer le sens de déplacement des porteurs de charge.

Cliquez pour accéder à une zone de dessin

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

33
Batterie lithium‑ion

✔ RAI/ANA : Utiliser et interpréter des documents

Doc.
Batterie lithium‑ion embarquée

Illustration de l'étiquette d'une batterie lithium-ion PowerBrick +12 : 12,8V, 12Ah, 153,6Wh. Certifiée CE et RoHS.

1. Relever la tension à vide E de cette batterie.

2. Préciser sa capacité électrique.

3. Expliquer ce que représente la valeur 153{,}6 W⋅h.

Dessin d'avion électrique, ailes déployées, deux hélices visibles.

Les avions électriques arrivent déjà sur le marché : en 2019, la start‑up israélienne Eviation a présenté son jet électrique capable de transporter neuf personnes. Sa batterie lithium‑ion lui permettrait de voler jusqu'à 450 km⋅h^-1 avec une autonomie de 1 000 km.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

34
Pile nickel‑cadmium

✔ VAL : Faire preuve d'esprit critique

D'après le sujet Bac S, Polynésie, 2010.

On considère une pile \text{Ni-Cd} constituée de deux demipiles reliées entre elles par un pont salin et qui met en jeu les couples \text{Ni}^{2+}\text{(aq)/Ni(s)} et \text{Cd}^{2+}\text{(aq)/Cd(s)}. Chaque demi‑pile contient 20 mL d'électrolyte.
On propose l'équation de réaction suivante :

\mathrm{Cd}^{2+}(\mathrm{aq})+\mathrm{Ni}(\mathrm{s}) \rightleftarrows \mathrm{Cd}(\mathrm{s})+\mathrm{Ni}^{2+}(\mathrm{aq})

1. Calculer le quotient de réaction à l'état initial Q_\text{r,i}.

2. En déduire le sens d'évolution spontanée du système chimique constituant la pile.

3. Indiquer la polarité des électrodes de nickel et de cadmium.

4. Préciser le rôle du pont salin.

Données

Concentration des électrolytes : c_\text{i} = 0{,}10 mol⋅L^-1
Constante d'équilibre à \bold{298 K} : K = 2{,}2 \times 10^{-6}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Mesure d'une constante de réaction

✔ VAL : Exploiter un ensemble de mesures

On cherche à déterminer la constante de formation du thiocyanate de fer III :

\mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{SCN}^{-}(\mathrm{aq}) \rightleftharpoons[\mathrm{FeSCN}]^{2+}(\mathrm{aq})

Pour cela, on mélange un volume V_1 = 10{,}0 mL d'une solution de nitrate ferrique (\mathrm{Fe}^{3+}(\mathrm{aq})~; 3\mathrm{NO}_{3}^{-}(\mathrm{aq})) de concentration c_1 = 2{,}5 \times 10^{-2} mol·L^-1 et un volume V_2 = 10{,}0 mL d'une solution de thiocyanate de potassium \mathrm{K}^{+}(\mathrm{aq})~; \mathrm{SCN}^{-}(\mathrm{aq})) de concentration c_2 = 2{,}5 \times 10^{-4} mol·L^-1.
À la longueur d'onde de 450 nm, seul l'ion [\mathrm{FeSCN}]^{2+}(\mathrm{aq}) a une absorption significative. On mesure l'absorbance de la solution à l'état final, on trouve A_f = 0{,}496.

1. Exprimer la constante d'équilibre de la réaction K en fonction des concentrations à l'état final.

2. À l'aide d'un tableau d'avancement, exprimer les concentrations à l'état final en fonction de l'avancement final x_f.

Cliquez pour accéder à une zone de dessin

3. Exprimer l'avancement final x_fen fonction de l'absorbance A_f à l'état final.

4. Déterminer la constante d'équilibre K de cette réaction.

Données

Coefficient d'absorption molaire de l'ion \bm{[\bf{FeSCN}]^{2+}(\bf{aq})} à 450 nm : \epsilon = 6{,}5 \times 10^3 L·mol^-1·cm^-1.
Largeur de la cuve utilisée : l = 1{,}0 cm

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Pile Daniell

✔ REA : Appliquer une formule

En 1836, le chimiste britannique John Daniell invente une pile électrique constituée d'une lame de zinc plongée dans une solution de sulfate de zinc (l'anode) et d'une lame de cuivre plongée dans une solution de sulfate de cuivre (la cathode). Les deux solutions sont reliées par un pont salin. L'équation de fonctionnement est :

\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \rightleftharpoons \mathrm{Zn}^{2+}(\mathrm{aq})+\mathrm{Cu}(\mathrm{s})

Sa constante d'équilibre est égale à K = 1{,}9 \times 10^{37}.

1. Déterminer le sens d'évolution spontanée et justifier que l'électrode de zinc est bien l'anode et l'électrode de cuivre la cathode.

2. Justifier que la réaction peut être considérée totale.

On considère une pile Daniell dont les caractéristiques sont celles fournies dans les données.

3. Identifier le réactif limitant.

4. Calculer la capacité électrique de cette pile.

Données

Couples d'oxydo‑réduction : \mathrm{Zn}^{2+}(\mathrm{aq}) / \mathrm{Zn}(\mathrm{s}) et \mathrm{Cu}^{2+}(\mathrm{aq}) / \mathrm{Cu}(\mathrm{s})
Masse de la lame de cuivre : m_{Cu} = 10 g
Masse de la lame de zinc : m_{Zn} = 12 g
Concentration de la solution de sulfate de cuivre : [\text{Cu}^{2+}]_i = 1{,}0 mol·L^-1
Volume de la solution de sulfate de cuivre \bm{\left(\mathrm{Cu}^{2+}(\mathrm{aq})~; \mathrm{SO}_{4}{ }^{2-}(\mathrm{aq})\right)} : V_{ca} = 250 mL
Concentration de la solution de sulfate de zinc \bm{\left(\mathrm{Zn}^{2+}(\mathrm{aq}) ; \mathrm{SO}_{4}{ }^{2-}(\mathrm{aq})\right)} : [\text{Zn}^{2+}]_i = 1{,}0 mol·L^-1
Volume de la solution de sulfate de zinc : V_{an} = 250 mL

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Physique-Chimie Terminale Spécialité

Pour s'entraîner

22Pile saline contre pile alcaline

23Pile argent‑zinc

Détails du barème TOTAL /6 pts

24Pile de Volta

25Caractéristique d'une pile

26Vitamine C

27Question de taille

28Piles qui chauffent

29 Copie d'élève à commenter

30Générateur d'électricité

31Dosage et durée de fonctionnement

32Sens d'évolution d'une pile

33Batterie lithium‑ion

34Pile nickel‑cadmium

AMesure d'une constante de réaction

BPile Daniell

Une erreur sur la page ? Une idée à proposer ?

22
Pile saline contre pile alcaline

23
Pile argent‑zinc

Détails du barème
TOTAL /6 pts

24
Pile de Volta

25
Caractéristique d'une pile

26
Vitamine C

27
Question de taille

28
Piles qui chauffent

29

Copie d'élève à commenter

30
Générateur d'électricité

31
Dosage et durée de fonctionnement

32
Sens d'évolution d'une pile

33
Batterie lithium‑ion

34
Pile nickel‑cadmium

A
Mesure d'une constante de réaction

B
Pile Daniell