Construire les gammes

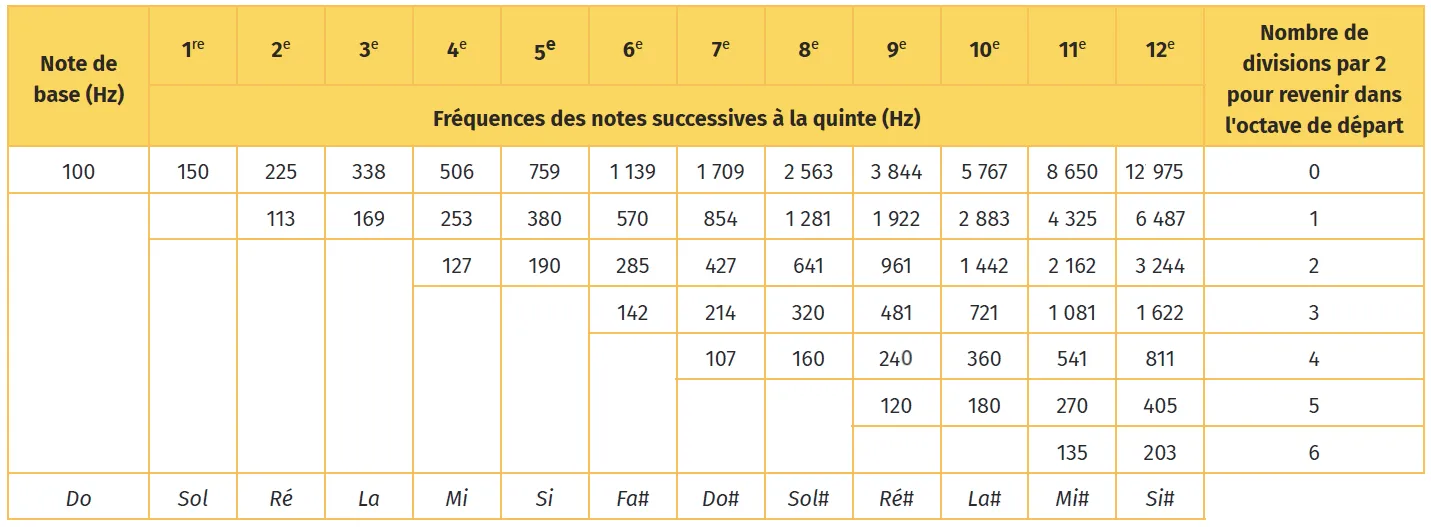
Pythagore veut créer une gamme, c'est-à-dire un nombre précis de notes. Seul problème : il y a une infinité de sons possibles. Il propose alors de partir de la corde entière, puis de prendre la quinte, puis la quinte de la quinte, puis la quinte de la quinte de la quinte et ainsi de suite. Si la fréquence de la corde entière vaut 1, alors la fréquence de l'octave vaut le double, soit deux. On cherche donc les quintes dont la fréquence est comprise entre 1 et 2. Prenons une corde qui fait sonner un do.

La première quinte vaut \dfrac{3}{2}= 1,5. C'est le sol.

La deuxième quinte de la quinte vaut \dfrac{3}{2} \times \dfrac{3}{2}, c'est-à-dire \dfrac{3^{2}}{2^{2}}= 2,25 ; c'est au-delà de 2 (l'octave) ; on divise donc par deux cette fréquence pour la ramener dans notre octave de départ : on obtient alors 1,125. C'est le ré ! La troisième quinte vaut \dfrac{3^{3}}{2^{3}}= 3,38.

On la ramène dans l'octave en divisant par deux ce qui donne : 1,69. C'est le la.

La quatrième quinte vaut \dfrac{3^{4}}{2^{4}}= 5,06. On divise par deux : 2,53. C'est encore trop donc on divise à nouveau par deux : 1,256. C'est le mi. On continue comme cela jusqu'à la douzième quinte qui vaut \dfrac{3^{12}}{2^{12}}= 129,75 que l'on réduit en divisant par deux six fois de suite pour obtenir 2,03.

C'est, à très peu de chose près, la fréquence de l'octave ! Cela signifie qu'en prenant douze fois de suite la quinte, on crée douze notes, la douzième étant l'octave de la première. Il ne reste plus qu'à mettre les fréquences dans l'ordre des fréquences croissantes (de la plus petite à la plus grande) pour obtenir les douze notes de la gamme chromatique.