Chapitre 11
Entrainement 2
Événement d'une expérience aléatoire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
[Chercher.]
Le jeu de Scrabble® est composé de 102 jetons : 2 jokers qui rapportent 0 point et les 26 lettres de l'alphabet qui sont réparties de la façon suivante.

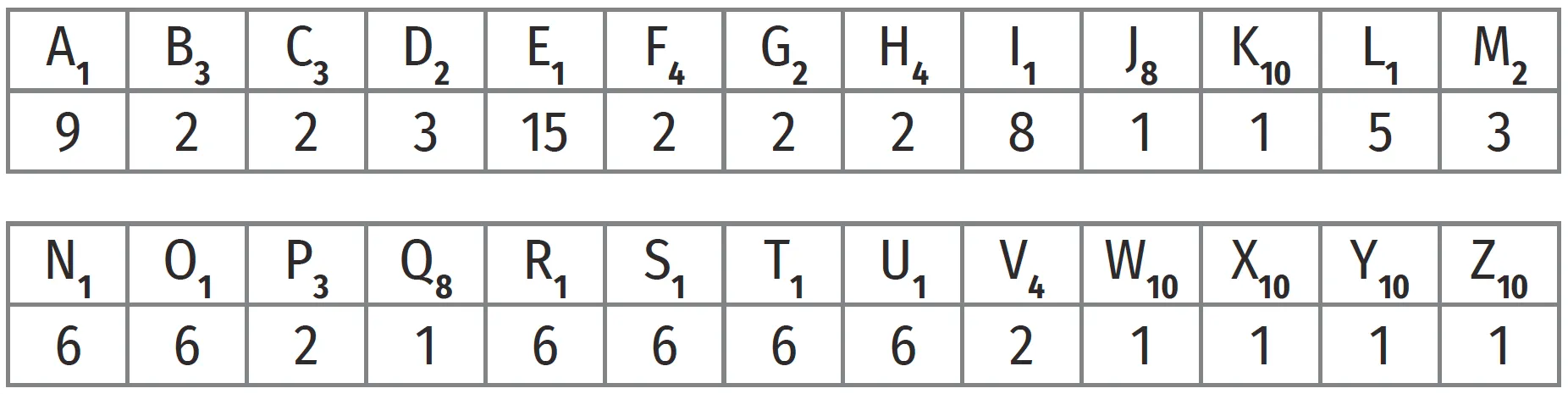
Par exemple, 9 jetons portent la lettre A et rapportent 1 point chacun, 2 jetons portent la lettre B et rapportent 3 points chacun, 2 jetons portent la lettre C et rapportent 3 points chacun, etc. On tire au hasard un jeton de Scrabble®. Quelle est la probabilité de tirer :
1. une voyelle ?
2. une lettre qui rapporte 10 points ?
3. une lettre du mot « PROBA » ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
[Chercher.]
Le jeu d'échecs est composé de 16 pièces blanches et de 16 noires réparties comme suit : un roi, une dame, deux fous, deux cavaliers, deux tours et huit pions. Les pièces mineures sont le fou et le cavalier alors que les pièces lourdes sont la dame et la tour.


1. un pion ?
2. une pièce mineure ?
3. une pièce lourde ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
[Chercher.]
Un jeu de tarot comporte 78 cartes :
- 56 cartes « classiques » (14 de chaque couleur : roi ; dame ; cavalier ; valet ; 10 \: ; 9 \: ; 8 \: ; 7 \: ; 6 \: ; 5 \: ; 4 \: ; 3 \: ; 2 \: ; as) ;
- 21 atouts (numérotés de 1 à 21) ;
- un joker appelé « excuse ».
Lors du comptage des points à la fin d'une partie, les cartes n'ont pas la même valeur :
- un roi, l'atout 1, l'atout 21 et l'excuse rapportent 4\text{,}5 points ;
- une dame rapporte 3\text{,}5 points ;
- un cavalier rapporte 2\text{,}5 points ;
- un valet rapporte 1\text{,}5 points ;
- toutes les autres cartes rapportent 0\text{,}5 point.
On tire une carte au hasard. Quelle est la probabilité de tirer :
1. une carte noire ?
2. une carte qui rapporte moins d'un point ?
3. une carte qui rapporte plus de 2 points ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Communiquer.] 

On considère un dé icosaédrique, dont les faces sont numérotées de 1 à 20, que l'on suppose bien équilibré. On lance le dé et on considère les événements :
- \text{A} : « on obtient un nombre pair » ;
- \text{B} : « on obtient un diviseur de 20 » ;
- \text{C} : « on obtient un multiple de 4 ».
Écrire chaque événement sous forme d'un ensemble des issues possibles et calculer leur probabilité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
[Représenter.]
On suppose que lorsqu'un couple attend un enfant, il est aussi probable qu'il s'agisse d'une fille ou d'un garçon.
1. Représenter, à l'aide d'un arbre, les possibilités pour
une famille de 3 enfants.
Cliquez pour accéder à une zone de dessin
2. Quelle est la probabilité de n'avoir que des garçons ?
3. Quelle est la probabilité d'avoir une fille en dernier ?
4. Quelle est la probabilité d'avoir deux garçons ?
3. Quelle est la probabilité d'avoir une fille en dernier ?
4. Quelle est la probabilité d'avoir deux garçons ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Modéliser.]
Une épreuve d'un concours est un Vrai/Faux de 4 questions. Un candidat répond au hasard à ces 4 questions.
1. Représenter, à l'aide d'un arbre, les différentes
réponses possibles.
Cliquez pour accéder à une zone de dessin
2. On suppose à présent que toutes les affirmations
sont vraies. En répondant au hasard :
a. quelle est la probabilité de n'avoir que des bonnes réponses ?
b. quelle est la probabilité de n'avoir qu'une seule bonne réponse ?
c. quelle est la probabilité d'avoir au moins 2 bonnes réponses ?
d. quelle est la probabilité d'avoir bien répondu à la troisième question ?
a. quelle est la probabilité de n'avoir que des bonnes réponses ?
b. quelle est la probabilité de n'avoir qu'une seule bonne réponse ?
c. quelle est la probabilité d'avoir au moins 2 bonnes réponses ?
d. quelle est la probabilité d'avoir bien répondu à la troisième question ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
Dans la population mondiale, les groupes sanguins sont répartis selon le tableau ci-dessous.

Grâce aux données de ce tableau, si on choisit au hasard une personne dans la population mondiale, quelle est la probabilité qu'elle soit :
1. donneur universel, c'est-à-dire qu'elle soit du groupe O et de rhésus − ?
2. du groupe AB ?
3. de rhésus + ?
2. du groupe AB ?
3. de rhésus + ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Chercher.] À la bataille navale, chaque joueur a une flotte composée de cinq bateaux : un porte-avions (5 cases), un croiseur (4 cases), un contre-torpilleur (3 cases), un sous-marin (3 cases) et un torpilleur (2 cases). Un joueur a disposé ses bateaux comme représentés ci-après. Les bateaux sont obligatoirement disposés horizontalement ou verticalement.

L'autre joueur choisit de tirer sur une case au hasard.
1. Quelle est la probabilité qu'il touche un bateau ?
2. Quelle est la probabilité qu'il touche un bateau s'il décide de ne tirer que dans les colonnes D et H ?
3. Au tour précédent, il a touché la case D4. Quelle est la probabilité de toucher à nouveau le croiseur en jouant correctement ?
2. Quelle est la probabilité qu'il touche un bateau s'il décide de ne tirer que dans les colonnes D et H ?
3. Au tour précédent, il a touché la case D4. Quelle est la probabilité de toucher à nouveau le croiseur en jouant correctement ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
[Chercher.]
Dans un zoo, on a regroupé dans le même enclos deux dromadaires (\text{D}_1 et \text{D}_2), deux chameaux ( \text{C}_1 et \text{C}_2) et un lama (\text{L}). Un visiteur prend une photo de trois animaux côte à côte qui ont tous la même probabilité d'être photographiés.
Quelle est la probabilité que le visiteur ait photographié quatre bosses ?
Quelle est la probabilité que le visiteur ait photographié quatre bosses ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
Voici la répartition, par sexe et par classes d'âges, de la population de la France au début de l'année 2019.
| Âges | Hommes | Femmes |
| 0 à 14 ans | 6 139 574 | 5 879 846 |
| 15 à 29 ans | 5 893 527 | 5 794 778 |
| 30 à 44 ans | 6 064 732 | 6 333 430 |
| 45 à 59 ans | 6 561 825 | 6 823 496 |
| 60 à 74 ans | 5 315 168 | 5 967 475 |
| 75 ans ou plus | 2 419 705 | 3 799 143 |
| Total | 32 394 531 | 34 598 168 |
Source : Insee (https://www.insee.fr/fr/statistiques/2381474)
On choisit au hasard une personne parmi la population
française. En arrondissant le résultat à 10^{-2} près, calculer
la probabilité que :
1. cette personne soit un homme ;
2. cette personne soit une femme de plus de 75 ans ;
3. cette personne soit un homme de moins de 30 ans ;
4. cette personne ait plus de 60 ans.
1. cette personne soit un homme ;
2. cette personne soit une femme de plus de 75 ans ;
3. cette personne soit un homme de moins de 30 ans ;
4. cette personne ait plus de 60 ans.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Calculer.] 
Un jeu consiste à tirer dans la cible ci-dessus.
- La zone rouge est un cercle de rayon 10 cm.
- La zone orange est une couronne dont le grand rayon est 30 cm.
- La zone jaune est une couronne dont le grand rayon est 50 cm.
- La zone bleue est une couronne dont le grand rayon est 70 cm.
La probabilité d'atteindre une zone est proportionnelle à sa surface. On suppose que le participant ne rate jamais la cible. Quelles sont les probabilités d'atteindre les différentes zones ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Chercher.]


Un Rubik's cube est constitué de 27 petits cubes sur lesquels sont collés des étiquettes de couleur. On détache les petits cubes, indiscernables au toucher, et on les places dans une urne. On en tire un au hasard. Quelle est la probabilité de tirer un petit cube avec :
1. aucune face colorée ?
2. une seule face colorée ?
3. trois faces colorées ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Chercher.]
Pour choisir le prénom de leur futur enfant, un couple regarde le calendrier du mois de novembre et il choisit un jour au hasard. On admet que la méthode utilisée par le couple pour choisir un jour de novembre représente une situation d'équiprobabilité.
1. Quelle est la probabilité de tomber sur un jour impair ?
2. Quelle est la probabilité de tomber sur un jour où apparaît le chiffre 1 \: ?
3. Quelle est la probabilité de tomber sur un jour férié ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
[Modéliser.]
Une urne contient deux boules rouges (\text{R}_1 et \text{R}_2) et trois boules noires (\text{N}_1, \text{N}_2 et \text{N}_3) toutes indiscernables au toucher. On tire successivement et avec remise deux boules dans l'urne et on considère les événements :
- \text{A} : « les deux boules sont de même couleur » ;
- \text{B} : « la première boule tirée est rouge ».
Écrire chaque événement sous forme d'un ensemble des issues possibles et calculer leur probabilité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Modéliser.]
Une urne contient deux boules vertes (\text{V}_1 et \text{V}_2) et trois boules noires (\text{N}_1, \text{N}_2 et \text{N}_3) toutes indiscernables au toucher. On tire successivement et sans remise deux boules dans l'urne et on considère les événements :
- \text{A} : « les deux boules sont de même couleur » ;
- \text{B} : « au moins une boule est verte ».
Écrire chaque événement sous forme d'un ensemble des issues possibles et calculer leur probabilité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
[Modéliser.] Dans une urne, on place six jetons sur lesquels sont inscrites les lettres du mot « BOSTON ». On pioche un jeton au hasard. On considère les événements :
- \text{A}\: : « on obtient une voyelle » ;
- \text{B}\: : « on obtient une lettre du mot PROBABILITÉS » ;
- \text{C}\: : « on obtient une lettre du mot FONCTION » ;
- \text{D}\: : « on obtient une lettre du mot MILIEU ».
Écrire chaque événement sous forme d'un ensemble des issues possibles et calculer leur probabilité.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

