Préparer la Première
Probabilités et statistiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Dans un lycée de 750 élèves, le tableau ci-dessous indique les effectifs d'élèves inscrits en espagnol par niveau.
On sait aussi que 4 % des hispanistes apprennent le latin. Chez les non-hispanistes, ce pourcentage est de 8 %.
| Seconde | Première | Terminale |
| 240 | 223 | 212 |
On sait aussi que 4 % des hispanistes apprennent le latin. Chez les non-hispanistes, ce pourcentage est de 8 %.
1. En moyenne, combien d'élèves sont inscrits en espagnol par niveau ?
2. Quel pourcentage d'élèves apprennent l'espagnol ?
3. Si on choisit un élève de ce lycée au hasard, calculer la probabilité :
a. \text{P}(\text{L}) qu'il apprenne le latin ;
b. qu'il apprenne l'espagnol et le latin ;
2. Quel pourcentage d'élèves apprennent l'espagnol ?
3. Si on choisit un élève de ce lycée au hasard, calculer la probabilité :
a. \text{P}(\text{L}) qu'il apprenne le latin ;
b. qu'il apprenne l'espagnol et le latin ;
c. qu'il apprenne l'espagnol ou le latin.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Dans un petit magasin, en novembre 2019, sept chemises différentes sont vendues aux prix suivants
donnés en euros : 39 \: ; 59 \: ; 24 \: ; 13 \: ; 67 \: ; 50 \: ; 42.
1. Calculer le prix moyen des chemises \overline { x _ { \mathrm { N } } } et l'écart-type \sigma _ { \mathrm { N } } en novembre 2019. Arrondir au dixième.
2. En décembre, à l'approche de Noël, le gérant décide d'augmenter les prix de toutes les chemises de 20 %. Calculer les nouveaux prix.
3. Calculer le prix moyen des chemises \overline { x _ { \mathrm { D } } } et l'écart-type \sigma _ { \mathrm { D } } en décembre 2019. Arrondir au dixième.
5. En janvier 2020, le gérant diminue tous ses prix de 20 %. Quel est le coefficient multiplicateur associé à cette baisse ?
6. Sans déterminer les nouveaux prix, calculer le prix moyen des chemises \overline { x _ { \mathrm { J } } } en janvier 2020.
7. Calculer le taux d'évolution des prix entre novembre 2019 et janvier 2020 de deux façons différentes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Dans un lycée, en juin 2019, parmi les 400 élèves de seconde, 60 % s'orientent en première générale.
Parmi eux, il y a 45 % de garçons. Les autres élèves s'orientent en première technologique et, parmi eux, 45 % sont des filles. 1. En septembre 2019, on tire un élève de première au hasard : quelle est la probabilité que ce soit un garçon ?
2. En juin 2020, les effectifs de seconde sont 25 % plus importants que l'année précédente. 125 garçons et 115 filles s'orientent en première technologique. 140 filles s'orientent en première générale. On considère que le reste des élèves de seconde sont des garçons s'orientant en première générale : combien sont-ils ?
3. Quel est le taux d'évolution d'élèves inscrits en première technologique entre septembre 2019 et septembre 2020 ?
Parmi eux, il y a 45 % de garçons. Les autres élèves s'orientent en première technologique et, parmi eux, 45 % sont des filles. 1. En septembre 2019, on tire un élève de première au hasard : quelle est la probabilité que ce soit un garçon ?
2. En juin 2020, les effectifs de seconde sont 25 % plus importants que l'année précédente. 125 garçons et 115 filles s'orientent en première technologique. 140 filles s'orientent en première générale. On considère que le reste des élèves de seconde sont des garçons s'orientant en première générale : combien sont-ils ?
3. Quel est le taux d'évolution d'élèves inscrits en première technologique entre septembre 2019 et septembre 2020 ?
4. En septembre 2020, on tire deux élèves de première au hasard et on note si ce sont des garçons ou des filles. Construire l'arbre pondéré de cette expérience aléatoire.
5. On s'intéresse maintenant à la filière (générale ou technologique) de ces deux élèves. Quelle est la probabilité qu'ils soient dans la même filière ? Ici, comme le nombre d'élèves est grand, on pourra considérer cette expérience comme un tirage avec remise.
Cliquez pour accéder à une zone de dessin
5. On s'intéresse maintenant à la filière (générale ou technologique) de ces deux élèves. Quelle est la probabilité qu'ils soient dans la même filière ? Ici, comme le nombre d'élèves est grand, on pourra considérer cette expérience comme un tirage avec remise.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Cent tickets de tombola sont vendus lors d'une kermesse. Un ticket super-gagnant offre 100 €, et dix tickets gagnants offrent 5 € chacun. Les autres sont perdants. On achète un ticket. 1. Calculer la probabilité de tirer le ticket super-gagnant puis la probabilité d'en tirer un simplement gagnant.
2. En déduire la probabilité de tirer un ticket perdant.
3. Compléter le tableau des effectifs ci-dessous.
| Gain (en €) | 0 | 5 | 100 |
| Effectif |
4. Compléter la loi de probabilité ci-dessous.
| Gain (en €) | 0 | 5 | 100 |
| Probabilité |
5. Calculer le gain moyen par ticket.
6. Chaque ticket de tombola coûte 2 €. On appelle espérance du jeu la différence entre le gain moyen et le coût du jeu. Calculer l'espérance de celui-ci et en déduire s'il est rentable d'acheter un ticket lors de cette tombola.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
On considère la série \text{S} : 3 \: ; 4 \: ; 5 \: ; 6 \: ; 10.
1. Déterminer la médiane \text{Me}, le 1er quartile \text{Q}_1, le 3e quartile \text{Q}_3 et l'écart interquartile e.
2. On considère la série \text {S} ^ { \prime } dont les valeurs sont celles de \text {S} multipliées par 2. Déterminer sa médiane \text {Me} ^ { \prime }, ses quartiles \text {Q}_{1} ^ { \prime } et \text {Q}_{3} ^ {\prime } et son écart interquartile e^ { \prime }.
3. Exprimer \text {Me} ^ { \prime }, \text {Q}_{1} ^ { \prime }, \text {Q}_{3} ^ {\prime } et e^ { \prime } en fonction de \text{Me}, \text{Q}_1, \text{Q}_3 et e.
4. Démontrer que, pour une série dont l'effectif total est impair, quand on multiplie ses valeurs par un nombre k , les indicateurs calculés en 2. sont aussi multipliés par k .
5. Une librairie papeterie vend sept sortes de cahiers aux prix HT suivants, en euros : 11 \: ; 10 \: ; 9 \: ; 8 \: ; 6 \: ; 10 \: ; 9.
Elle vend sept sortes de livres aux prix HT suivants, en euros : 3 \: ; 20 \: ; 3 \: ; 23 \: ; 9 \: ; 6 \: ; 21. Déterminer le prix médian des cahiers, puis celui des livres.
2. On considère la série \text {S} ^ { \prime } dont les valeurs sont celles de \text {S} multipliées par 2. Déterminer sa médiane \text {Me} ^ { \prime }, ses quartiles \text {Q}_{1} ^ { \prime } et \text {Q}_{3} ^ {\prime } et son écart interquartile e^ { \prime }.
3. Exprimer \text {Me} ^ { \prime }, \text {Q}_{1} ^ { \prime }, \text {Q}_{3} ^ {\prime } et e^ { \prime } en fonction de \text{Me}, \text{Q}_1, \text{Q}_3 et e.
4. Démontrer que, pour une série dont l'effectif total est impair, quand on multiplie ses valeurs par un nombre k , les indicateurs calculés en 2. sont aussi multipliés par k .
6. Calculer l'écart interquartile des deux séries ci-dessus puis comparer ces séries de prix.
7. Pour calculer le prix TTC de ces articles, on applique une TVA de 20 % sur les cahiers et de 5 % sur les livres. Ce sont donc des hausses de prix. Calculer les nouvelles médianes de ces séries de prix.
8. Calculer les nouveaux écarts interquartiles puis comparer les deux nouvelles séries de prix.
Ouverture SES : Que signifient les acronymes HT, TTC et TVA ? Les taux de TVA sont-ils différents selon les produits ? Donner d'autres exemples.
7. Pour calculer le prix TTC de ces articles, on applique une TVA de 20 % sur les cahiers et de 5 % sur les livres. Ce sont donc des hausses de prix. Calculer les nouvelles médianes de ces séries de prix.
8. Calculer les nouveaux écarts interquartiles puis comparer les deux nouvelles séries de prix.
Ouverture SES : Que signifient les acronymes HT, TTC et TVA ? Les taux de TVA sont-ils différents selon les produits ? Donner d'autres exemples.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
On a mesuré un enfant tous les mois lors de sa 1re année et notifié les valeurs obtenues en cm dans un
tableau.

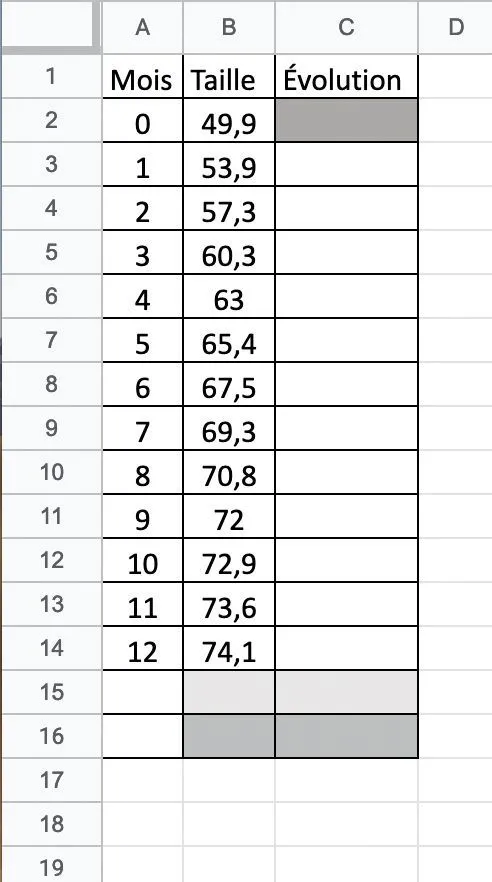


1. Quelle formule
faut-il entrer dans la cellule C3 puis étirer vers le bas afin de calculer tous les taux d'évolution de la taille
par mois ?
2. Calculer ces 12 taux mensuels d'évolution. Exprimer les taux en pourcentage, arrondis au dixième.
3. Calculer la moyenne puis la médiane des taux mensuels d'évolution.
4. Interpréter la valeur de la médiane.
5. a. Calculer le taux d'évolution sur l'année complète. Exprimer ce taux en pourcentage.
b. Déduire de ce résultat le taux d'évolution moyen de la taille de ce bébé par mois. Écrire le résultat en pourcentage arrondi au centième.
2. Calculer ces 12 taux mensuels d'évolution. Exprimer les taux en pourcentage, arrondis au dixième.
3. Calculer la moyenne puis la médiane des taux mensuels d'évolution.
4. Interpréter la valeur de la médiane.
b. Déduire de ce résultat le taux d'évolution moyen de la taille de ce bébé par mois. Écrire le résultat en pourcentage arrondi au centième.
6. Soient x le coefficient multiplicateur associé au taux mensuel d'évolution de la taille et \text{V}_\text{D} la taille du bébé à la naissance. Exprimer, en fonction de x et de \text{V}_\text{D}, la taille du bébé \text{V}_\text{A} après 12 mois.
7. On donne \text{V}_\text{D}=49\text{,}9 cm : calculer les trois valeurs de \text{V}_\text{A} possibles lorsqu'on remplace x par les deux valeurs trouvées en 3. puis celle trouvée en 5. b. Arrondir au dixième de cm.
8. En déduire le taux mensuel d'évolution de la taille d'un bébé qui vous semble le plus approprié au cours de sa première année.


7. On donne \text{V}_\text{D}=49\text{,}9 cm : calculer les trois valeurs de \text{V}_\text{A} possibles lorsqu'on remplace x par les deux valeurs trouvées en 3. puis celle trouvée en 5. b. Arrondir au dixième de cm.
8. En déduire le taux mensuel d'évolution de la taille d'un bébé qui vous semble le plus approprié au cours de sa première année.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Mme Pelard, professeure de mathématiques, passe voir chacun de ses 20 élèves de seconde avec une bobine de fil.
Elle demande à chacun d'entre eux de couper un morceau de fil dont ils estiment la longueur à 10 cm, le tout sans pouvoir mesurer. Elle récupère tous les bouts de fil et les mesure.
Voici les longueurs en cm : 10 \: ; 11 \: ; 9 \: ; 9\text{,}5 \: ; 10\text{,}5 \: ; 11\text{,}8 \: ; 9\text{,}2 \: ; 10\text{,}6 \: ; 9\text{,}4 \: ; 11\text{,}8 \: ; 10\text{,}1 \: ; 12\text{,}8 \: ; 8\text{,}3 \: ; 10\text{,}8 \: ; 12\text{,}3 \: ; 11\text{,}4 \: ; 13\text{,}7 \: ; 9\text{,}7 \: ; 8\text{,}9 \: ; 12.
Elle demande à chacun d'entre eux de couper un morceau de fil dont ils estiment la longueur à 10 cm, le tout sans pouvoir mesurer. Elle récupère tous les bouts de fil et les mesure.
Voici les longueurs en cm : 10 \: ; 11 \: ; 9 \: ; 9\text{,}5 \: ; 10\text{,}5 \: ; 11\text{,}8 \: ; 9\text{,}2 \: ; 10\text{,}6 \: ; 9\text{,}4 \: ; 11\text{,}8 \: ; 10\text{,}1 \: ; 12\text{,}8 \: ; 8\text{,}3 \: ; 10\text{,}8 \: ; 12\text{,}3 \: ; 11\text{,}4 \: ; 13\text{,}7 \: ; 9\text{,}7 \: ; 8\text{,}9 \: ; 12.
1. Calculer la médiane et l'écart interquartile de cette série.
2. Interpréter le résultat de la médiane.
3. Calculer la moyenne \overline { x } et l'écart-type \sigma. Arrondir au centième de cm.
4. Déterminer l'intervalle [ \overline { x } - 2 \sigma \: ; \overline { x } + 2 \sigma ].
5. Calculer la proportion de valeurs de la série comprises dans l'intervalle [ \overline { x } - 2 \sigma \: ; \overline { x } + 2 \sigma ].
2. Interpréter le résultat de la médiane.
3. Calculer la moyenne \overline { x } et l'écart-type \sigma. Arrondir au centième de cm.
4. Déterminer l'intervalle [ \overline { x } - 2 \sigma \: ; \overline { x } + 2 \sigma ].
6. Une étude de grande envergure a été réalisée sur
10 000 individus : on leur a demandé la même chose qu'aux élèves de Mme Pelard. Les morceaux de fil ont été mesurés au mm près.
a. Pourquoi peut-on conjecturer des probabilités grâce à cette étude ?
b. Si on demande à une personne de couper un morceau de fil de 10 cm sans mesure, quelle est la probabilité que ce morceau mesure exactement 0 cm ?
c. Selon vous, quelle est la probabilité que ce morceau de fil soit compris dans l'intervalle [ \overline { x } - 2 \sigma \: ; \overline { x } + 2 \sigma ] \: ?
- 250 personnes ont coupé un morceau de fil de 10 cm.
- \overline { x } = 10\text{,}8 cm et \sigma = 1\text{,}5 cm.
- 94,8 % des morceaux sont compris dans l'intervalle [ \overline { x } - 2 \sigma \: ; \overline { x } + 2 \sigma ].
a. Pourquoi peut-on conjecturer des probabilités grâce à cette étude ?
b. Si on demande à une personne de couper un morceau de fil de 10 cm sans mesure, quelle est la probabilité que ce morceau mesure exactement 0 cm ?
c. Selon vous, quelle est la probabilité que ce morceau de fil soit compris dans l'intervalle [ \overline { x } - 2 \sigma \: ; \overline { x } + 2 \sigma ] \: ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

