Mathématiques Expertes Terminale
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 5
TP Info 1
Test de primalité de Fermat
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Utiliser un test probabiliste de primalité afin d'évaluer si un entier \boldsymbol{n} est premier ou non, à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
1. a. Dans un tableur, entrer la liste des 46 premiers nombres entiers strictement supérieurs à 2 dans la colonne A.
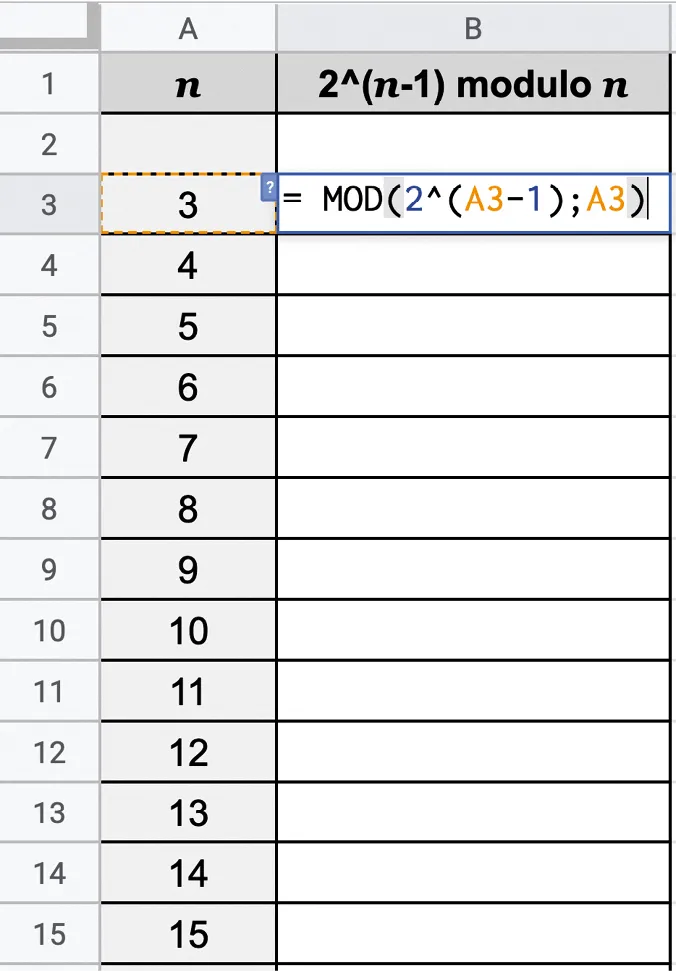
Dans la cellule B3, entrer la formule : =MOD(2^(A3-1);A3).
Étendre ensuite la formule à toute la colonne. (Fichier téléchargeable .)
Dans la cellule B3, entrer la formule : =MOD(2^(A3-1);A3).
Étendre ensuite la formule à toute la colonne. (Fichier téléchargeable .)
b. À quoi la commande MOD sert‑elle ?
2. D'après le petit théorème de Fermat, quel nombre est affiché dans la colonne B lorsque n est premier ?
3. Si une cellule de la colonne B n'est pas égale à 1, que peut‑on dire du nombre n correspondant ?
4. a. Lister l'ensemble des entiers n inférieurs à 46 dont la cellule de la colonne B est égale à 1.
Que remarque‑t‑on ?
b. Combien vaut 2^{40} modulo 561 ? En déduire 2^{560} [561]. Le nombre 561 est‑il premier ?
c. Finalement, que peut‑on dire lorsque la cellule de la colonne B est égale à 1 ?
2. D'après le petit théorème de Fermat, quel nombre est affiché dans la colonne B lorsque n est premier ?
3. Si une cellule de la colonne B n'est pas égale à 1, que peut‑on dire du nombre n correspondant ?
4. a. Lister l'ensemble des entiers n inférieurs à 46 dont la cellule de la colonne B est égale à 1.
Que remarque‑t‑on ?
b. Combien vaut 2^{40} modulo 561 ? En déduire 2^{560} [561]. Le nombre 561 est‑il premier ?
c. Finalement, que peut‑on dire lorsque la cellule de la colonne B est égale à 1 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
1. Dans la fonction ci‑dessous on considère un
entier n \geqslant 3.
À quoi sert la commande % ?
2. a. D'après le petit théorème de Fermat, que renvoie l'algorithme lorsque n est un nombre premier ?
b. Que peut‑on dire lorsque la valeur de F affichée en sortie d'algorithme n'est pas égale à 1 ?
c. Tester cet algorithme pour une dizaine de valeurs afin de vérifier les observations. Que remarque‑t‑on pour n=561 ? Cet entier est‑il premier ?
3. Les observations ci‑dessus servent à élaborer un test permettant de déterminer si le nombre n a des chances d'être premier.
a. Compléter la condition à tester ligne 3.
b. Tester l'algorithme avec quelques valeurs puis tester l'algorithme pour n=154 515 677.
c. Quel est l'avantage et l'inconvénient de cet algorithme par rapport à celui consistant à tester l'ensemble des diviseurs possibles entre 1 et \sqrt{n} ?
À quoi sert la commande % ?
2. a. D'après le petit théorème de Fermat, que renvoie l'algorithme lorsque n est un nombre premier ?
b. Que peut‑on dire lorsque la valeur de F affichée en sortie d'algorithme n'est pas égale à 1 ?
c. Tester cet algorithme pour une dizaine de valeurs afin de vérifier les observations. Que remarque‑t‑on pour n=561 ? Cet entier est‑il premier ?
3. Les observations ci‑dessus servent à élaborer un test permettant de déterminer si le nombre n a des chances d'être premier.
def testfermat2(n):
F = 2**(n-1) % n
if ... :
return("Peut-être premier")
else :
return ("Pas premier")
a. Compléter la condition à tester ligne 3.
b. Tester l'algorithme avec quelques valeurs puis tester l'algorithme pour n=154 515 677.
c. Quel est l'avantage et l'inconvénient de cet algorithme par rapport à celui consistant à tester l'ensemble des diviseurs possibles entre 1 et \sqrt{n} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les entiers p qui ne sont pas premiers mais qui vérifient a^{p-1} \equiv 1[p], dès lors que a et p sont premiers entre eux, sont appelés les nombres de Carmichael, du nom du mathématicien américain Robert Daniel Carmichael (1879‑1967), qui s'est tout particulièrement intéressé aux propriétés de ces nombres. Il a été démontré en 1994 qu'il existe en fait une infinité de nombres de Carmichael.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
